题目内容
【题目】在平面直角坐标系中,点O为坐标原点,我们把横、纵坐标都为整数的点称为整点,记定点都是整点的三角形为整点三角形.如图,已知整点O(0,0),A(2,4),请在所给网格区域(含边界)上按要求画图.
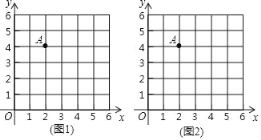
(1)在图1中画一个整点三角形OAB,其中点B在第一象限,且点B的横、纵坐标之和等于点A的横坐标;
(2)在图2中画一个整点三角形OAC,其中点C的坐标为(3t,t),且点C的横、纵坐标之和是点A的纵坐标的2倍.请直接写出△OAC的面积.
【答案】(1)详见解析;(2)10.
【解析】
(1) 由点A的横坐标为2, 且点B的横、 纵坐标之和等于点A的横坐标可得点B坐标为 (1, 1) , 据此可得;
(2) 由点A的纵坐标为4且点C的横、 纵坐标之和是点A的纵坐标的2倍可得3t+t=8, 解之得t=2, 据此知点C (6, 2) , 据此作图可得, 再根据割补法求解可得.
解:(1)如图所示,△OAB即为所求;
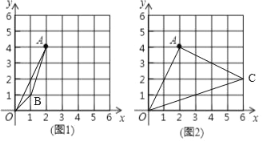
(2)如图所示,△OAC即为所求,
S△OAC=6×4﹣![]() ×2×4﹣
×2×4﹣![]() ×6×2﹣
×6×2﹣![]() ×2×4=10.
×2×4=10.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
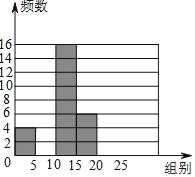
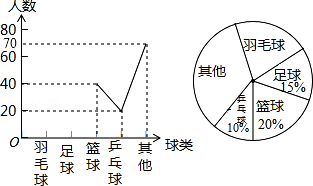
【题目】珠海市某中学开展主题为“我爱阅读”的专题调查活动,为了解学校1200名学生一年内阅读书籍量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
(1)a= ,b= c= .
(2)补全频数分布直方图;
(3)根据该样本,估计该校学生阅读书籍数量在15本或15本以上的人数.