题目内容
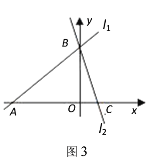
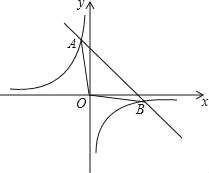
【题目】一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,m),B(n,﹣1)两点.
的图象相交于A(﹣1,m),B(n,﹣1)两点.
(1)求出这个一次函数的表达式.
(2)求△OAB的面积.
(3)直接写出使一次函数值大于反比例函数值的x的取值范围.
【答案】(1)一次函数的表达式为y=﹣x+1;(2)S△OAB=![]() ;(3)x<﹣1或0<x<2.
;(3)x<﹣1或0<x<2.
【解析】
(1)先把A(-1,m),B(n,-1)分别代入反比例函数解析式可求出m、n,于是确定A点坐标为(-1,2),B点坐标为(2,-1),然后利用待定系数法求直线AB的解析式;
(2)设直线AB交y轴于P点,先确定P点坐标,然后利用S△OAB=S△AOP+S△BOP和三角形面积公式进行计算;
(3)根据图象即可求得.
解:(1)把A(﹣1,m),B(n,﹣1)分别代入y=![]() 得﹣m=﹣2,﹣n=﹣2,解得m=2,n=2,
得﹣m=﹣2,﹣n=﹣2,解得m=2,n=2,
所以A点坐标为(﹣1,2),B点坐标为(2,﹣1),
把A(﹣1,2),B(2,﹣1)代入y=kx+b得![]() ,解得
,解得![]() ,
,
所以这个一次函数的表达式为y=﹣x+1;
(2)设直线AB交y轴于P点,如图,
当x=0时,y=1,所以P点坐标为(0,1),
所以S△OAB=S△AOP+S△BOP=![]() ×1×1+
×1×1+![]() ×1×2=
×1×2=![]() ;
;
(3)使一次函数值大于反比例函数值的x的取值范围是x<﹣1或0<x<2.


练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c(a≠0)图象上部分点的坐标(x,y)的对应值如下表所示:
x | … | 0 |
| 4 | … |
y | … | 0.37 | -1 | 0.37 | … |
则方程ax2+bx+1.37=0的根是( )
A.0或4B.![]() 或
或![]() C.1或5D.无实根
C.1或5D.无实根