Question

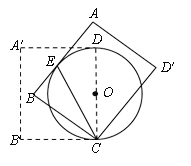
【题目】（阅读）如图1，在等腰△ABC中，AB=AC，AC边上的高为h，M是底边BC上的任意一点，点M到腰AB、AC的距离分别为h1，h2．连接AM．

∵ ∴

　　　　　　

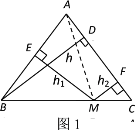
（思考）在上述问题中，h1，h2与h的数量关系为： ．

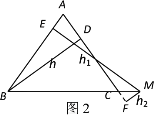
（探究）如图2，当点M在BC延长线上时，h1、h2、h之间有怎样的数量关系式？并说明理由．

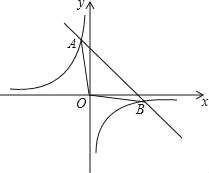
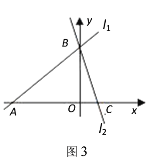
（应用）如图3，在平面直角坐标系中有两条直线l1：，l2：y=－3x+3，若l2上的一点M到l1的距离是1，请运用上述结论求出点M的坐标．

Answer 1

【答案】【思考】h1+h2=h；【探究】h1－h2=h．理由见解析；【应用】所求点M的坐标为（，2）或（－，4）．

【解析】

思考：根据等腰三角形的性质，把代数式化简可得.

探究：当点M在BC延长线上时，连接，可得，化简可得.

应用：先证明，△ABC为等腰三角形，即可运用上面得到的性质，再分点M在BC边上和在CB延长线上两种情况讨论，第一种有1+My=OB，第二种为My－1=OB，解得的纵坐标，再分别代入的解析式即可求解.

思考

即

h1+h2=h．

探究

h1－h2=h．

理由．连接,

∵

∴

∴h1－h2=h．

应用

在中，令x=0得y=3；

令y=0得x=－4，则：

A（－4，0），B（0，3）

同理求得C（1，0），

，

又因为AC=5，

所以AB=AC，即△ABC为等腰三角形．

①当点M在BC边上时，

由h1+h2=h得：

1+My=OB，My=3－1=2，

把它代入y=－3x+3中求得：

，

∴；

②当点M在CB延长线上时，

由h1－h2=h得：

My－1=OB，My=3+1=4，

把它代入y=－3x+3中求得：

，

∴，

综上，所求点M的坐标为或．