题目内容

B
考点:
分析:设正六边形的中心是O,一边是AB,过O作OG⊥AB与G,在直角△OAG中,根据三角函数即可求得边长AB,从而求出周长.
解答: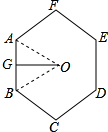
解:如图,在Rt△AOG中,OG=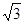 ,∠AOG=30°,
,∠AOG=30°,
∴cos30°=OG/AO,
∴OA=OG÷cos 30°=2.
这个正六边形的周长=12.
故选B.
点评:此题主要考查正多边形的计算问题,属于常规题.解题的关键是正确的构造直角三角形.
分析:设正六边形的中心是O,一边是AB,过O作OG⊥AB与G,在直角△OAG中,根据三角函数即可求得边长AB,从而求出周长.
解答:

解:如图,在Rt△AOG中,OG=
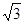 ,∠AOG=30°,
,∠AOG=30°,∴cos30°=OG/AO,
∴OA=OG÷cos 30°=2.
这个正六边形的周长=12.
故选B.
点评:此题主要考查正多边形的计算问题,属于常规题.解题的关键是正确的构造直角三角形.

练习册系列答案
相关题目
 为
为 的切线,
的切线,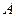 为切点,
为切点,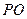 交
交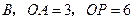 ,求
,求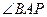 的度数.
的度数.
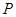 的正上方
的正上方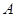 处,从
处,从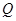 ,若∠
,若∠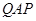 =
=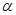 ,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
,地球半径为R,则航天飞机距地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( ) 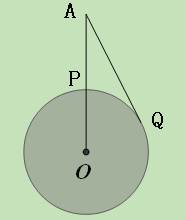
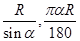
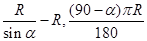
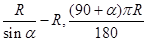
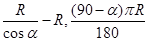
 线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作
线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作

 内接于⊙
内接于⊙ ,若
,若 =30°,
=30°, ,则⊙
,则⊙
 12分)如图,等圆⊙
12分)如图,等圆⊙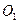 和⊙
和⊙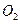 相交于A、B两点,⊙
相交于A、B两点,⊙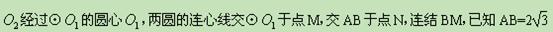
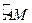 的长。
的长。

