Question

【题目】如图，已知AB是⊙O的直径，点C、D在⊙O的上，点E在⊙O的外，∠EAC＝∠D＝60°．

（1）求∠ABC的度数；

（2）求证：AE是⊙O的切线．

Answer 1

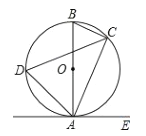
【答案】（1）∠ABC＝60°；（2）证明见解析．

【解析】

（1）利用圆周角定理，同弧所对圆周角相等圆周角，可证出∠ABC=∠D=60°，；

（2）根据AB是⊙O的直径，利用直径所对的圆周角是直角得到∠ACB=90°，在直角三角形中求出∠BAC=30°，从而推出∠BAE=90°，从而得AE是⊙O的切线；

（1）解：∵∠D＝60°，

∴∠ABC＝∠D＝60°；

（2）证明：∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠BAC＝90°﹣60°＝30°，

∴∠BAE＝∠BAC+∠EAC＝30°+60°＝90°，

∴BA⊥AE，

∴AE是⊙O的切线．