题目内容
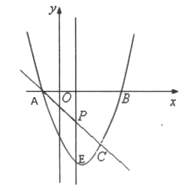
【题目】在平面直角坐标系中,已知抛物线y=![]() +bx﹣4经过A(﹣4,0),C(2,0)两点.
+bx﹣4经过A(﹣4,0),C(2,0)两点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,点B是抛物线与y轴交点.判断有几个位置能够使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

【答案】(1)y=![]() +x﹣4;(2) S=
+x﹣4;(2) S=![]() ﹣4m;m=﹣2时S有最大值S=4;(3)(﹣4,4)或(
﹣4m;m=﹣2时S有最大值S=4;(3)(﹣4,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)设抛物线解析式为y=![]() +bx+c,然后把点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
+bx+c,然后把点A、B、C的坐标代入函数解析式,利用待定系数法求解即可;
(2)根据图形的割补法,可得二次函数,根据抛物线的性质求出第三象限内二次函数的最值,然后即可得解;
(3)利用直线与抛物线的解析式表示出点P、Q的坐标,然后求出PQ的长度,再根据平行四边形的对边相等列出算式,然后解关于x的一元二次方程即可得解.
试题解析:(1)将A(﹣4,0),C(2,0)两点代入函数解析式,得
![]() ,
,
解得![]() ,
,
所以此函数解析式为:y=![]() +x﹣4;
+x﹣4;
(2)∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m,![]() +m﹣4),
+m﹣4),
∴![]() =
=![]() ×4×(
×4×(![]() +m﹣4)+
+m﹣4)+![]() ×4×(﹣m)﹣
×4×(﹣m)﹣![]() ×4×4=
×4×4=![]() ﹣4m=
﹣4m=![]() ,
,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4,
答:S关于 m的函数关系式为S=![]() ﹣4m;m=﹣2时S有最大值S=4;
﹣4m;m=﹣2时S有最大值S=4;
(3)∵点Q是直线y=﹣x上的动点,
∴设点Q的坐标为(a,﹣a),
∵点P在抛物线上,且PQ∥y轴,
∴点P的坐标为(a,![]() +a﹣4),
+a﹣4),
∴PQ=﹣a﹣(![]() +a﹣4)=
+a﹣4)=![]() ﹣2a+4,
﹣2a+4,
又∵OB=0﹣(﹣4)=4,
以点P,Q,B,O为顶点的四边形是平行四边形,
∴|PQ|=OB,
即|![]() ﹣2a+4|=4,
﹣2a+4|=4,
①![]() ﹣2a+4=4时,整理得,
﹣2a+4=4时,整理得,![]() +4a=0,
+4a=0,
解得a=0(舍去)或a=﹣4,
﹣a=4,
所以点Q坐标为(﹣4,4),
②![]() ﹣2a+4=﹣4时,整理得,
﹣2a+4=﹣4时,整理得,![]() +4a﹣16=0,
+4a﹣16=0,
解得a=![]() ,
,
所以点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
综上所述,Q坐标为(﹣4,4)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )时,使点P,Q,B,O为顶点的四边形是平行四边形.
)时,使点P,Q,B,O为顶点的四边形是平行四边形.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 40 | 60 | m |

(1)求n的值;
(2)统计表中的m= ;
(3)估计该校1800名学生中认为“影响很大”的学生人数.