Question

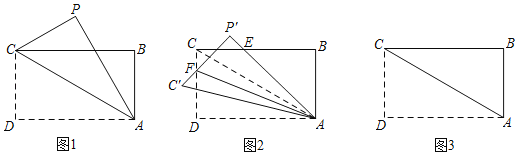
【题目】如图1，在矩形纸片ABCD中，AB＝2，AD＝6，将纸片沿对角线AC对折，点D落在点P处．

（1）填空：∠BCA的大小是　 　；

（2）如图2，吕家三少将折叠后的纸片沿着AC剪开，把△APC绕点A逆时针旋转α角（0°≤α≤90°），得到△AP′C′，点P，C分别对应点P′，C′，P′A交BC于点E，P′C′交CD于点F．

①点α＝15时，求证：AB＝BE；

②填空：当点P′落在边BC上时，连接AF，则tan∠DAF的值为　 　；

③填空：在②的条件下，将△AP′C′沿着AP′折叠至△AP′C″处，点C′对应点C″，AC″交BC于点G，则线段BG的长度为　 　．

Answer 1

【答案】（1）30°；（2）①详见解析；②③

【解析】

(1)求出∠ACB的正切值即可解决问题；

(2)①证明∠BAE＝45°即可解决问题；

②利用相似三角形的性质求出CF即可解决问题；

③如图3﹣2中，作GH⊥AP′于H，设GH＝x．构建方程求出x，再利用勾股定理求解即可．

(1)∵四边形ABCD是矩形，

∴∠B＝90°，AD＝BC＝6，AB＝CD＝2，

∴tan∠ACB＝，

∴∠ACB＝30°，

故答案为：30°；

(2)①如图2﹣1中，

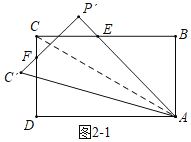
∵在Rt△ABC中，∠ACB＝30°，∠B＝90°，

∴∠CAB＝60°，

∵α＝15°，

∴∠CAE＝15°，

∴∠BAE＝45°，

∴∠AEB＝∠EAB＝45°，

∴BA＝BE；

②如图2﹣2中，

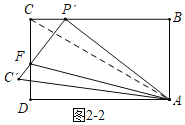
在Rt△ABP′中，BP′＝=2，

∴CP′＝6﹣2，

∵∠CFP′+∠FP′C＝90°，∠FP′C+∠AP′B＝90°，

∴∠AP′B＝∠CFP′，

∵∠FCP′＝∠B＝90°，

∴△FCP′∽△P′BA，

∴，

∴，

∴CF＝6﹣4，

∴DF＝2﹣(6﹣4)＝6﹣6，

∴tan∠DAF＝＝﹣，

故答案为：﹣；

③如图2-3中，作GH⊥AP′于H，设GH＝x，

由△P′HG∽△P′BA，可得P′H＝x，

∵∠GAH＝30°，∠GHA＝90°，

∴AH＝x，

∵AP′＝6，

∴x+x＝6，

∴x＝6(﹣)，

∴AG＝2GH＝12(﹣)，

在Rt△ABG中，BG＝＝8﹣18，

故答案为：﹣18．