题目内容
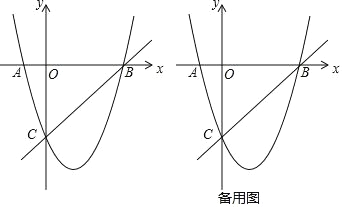
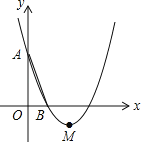
【题目】如图，在平面直角坐标系xOy中，已知抛物线y=x2+bx+c经过A（0，3），B（1，0）两点，顶点为M．
（1）求b、c的值；
（2）若只沿y轴上下平移该抛物线后与y轴的交点为A1，顶点为M1，且四边形AMM1A1是菱形，写出平移后抛物线的表达式．
【答案】（1）b=﹣4，c=3；（2）y=x2﹣4x+3+2
或y=x2﹣4x+3﹣2．
【解析】
（1）已知抛物线图象上A、B两点的坐标，将它们代入抛物线的解析式中，即可求得m、n的值；
（2）把解析式化成顶点式，求得顶点M的坐标，根据A、M的坐标，易求得AM的长；根据平移的性质知：若四边形A A′B′B为菱形，那么必须满足AA1=AM，由此可确定平移的距离，根据“上加下减”的平移规律即可求得平移后的抛物线解析式．
（1）抛物线y=x2+bx+c经过A（0，3），B（1，0）两点，则有：
解得
故b=﹣4，c=3．
（2）由（1）得：y=x2﹣4x+3=（x﹣2）2﹣1；
∴M（2，﹣1），
∵A（0，3），
∴AM=
=2，
由平移可知：AA1∥MM1，AA1=MM1，
当AA1=AM=2时，四边形AMM1A1是菱形，
故抛物线需向上或向下平移2个单位，即：
y=x2﹣4x+3+2或y=x2﹣4x+3﹣2．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
