题目内容
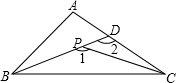
如图,在△ABC中,∠ABC、∠ACB的平分线交于点O.
(1)若∠ABC=40°,∠ACB=50°,则∠BOC=______
(2)若∠ABC+∠ACB=lO0°,则∠BOC=______.
(3)若∠A=70°,则∠BOC=______.
(4)若∠BOC=140°,则∠A=______.
(5)你能发现∠BOC与∠A之间有什么数量关系吗?写出并说明理由.

(1)若∠ABC=40°,∠ACB=50°,则∠BOC=______
(2)若∠ABC+∠ACB=lO0°,则∠BOC=______.
(3)若∠A=70°,则∠BOC=______.
(4)若∠BOC=140°,则∠A=______.
(5)你能发现∠BOC与∠A之间有什么数量关系吗?写出并说明理由.

(1)∵∠ABC=40°,∠ACB=50°,在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=
∠ABC=20°,∠OCB=
∠ACB=25°,
∴∠BOC=180°-∠OBC-∠OCB=180°-20°-25°=135°,
故答案是:135°;
(2)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=50°,
∴∠BOC=180°-
(∠ABC+∠ACB)=180°-50°=130°,
故答案是130°.
(3)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°,
∴∠BOC=180°-
(∠ABC+∠ACB)=180°-55°=125°,
故答案是125°;
(4)∵∠BOC=140°,
∴∠OBC+OCB=40°,
∵∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠ABC+∠ACB=2(∠OBC+OCB)=80°,
∴∠A=100°,
故答案是:100°;
(5)设∠BOC=α,
∴∠OBC+OCB=180°-α,
∵∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠ABC+∠ACB=2(∠OBC+OCB)=2(180°-α)=360°-2α,
∴∠A=180°-(ABC+∠ACB)=180°-(360°-2α)=2α-180°,
故∠BOC与∠A之间的数量关系是:∠A=2∠BOC-180°.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠OBC-∠OCB=180°-20°-25°=135°,
故答案是:135°;
(2)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-
| 1 |
| 2 |
故答案是130°.
(3)在△ABC中,∠ABC、∠ACB的平分线交于点O.
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |

∴∠BOC=180°-
| 1 |
| 2 |
故答案是125°;
(4)∵∠BOC=140°,
∴∠OBC+OCB=40°,
∵∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC+∠ACB=2(∠OBC+OCB)=80°,
∴∠A=100°,
故答案是:100°;
(5)设∠BOC=α,
∴∠OBC+OCB=180°-α,
∵∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABC+∠ACB=2(∠OBC+OCB)=2(180°-α)=360°-2α,
∴∠A=180°-(ABC+∠ACB)=180°-(360°-2α)=2α-180°,
故∠BOC与∠A之间的数量关系是:∠A=2∠BOC-180°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目