题目内容
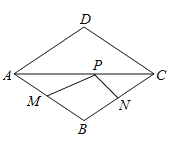
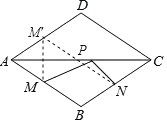
【题目】如图,点Р是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,![]() 的最小值是( )
的最小值是( )
A.1B.![]() C.2D.
C.2D.![]()
【答案】C
【解析】
先作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值.然后证明四边形ABNM′为平行四边形,即可求出MP+NP=M′N=AB=2.
解:如图,作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值,最小值为M′N的长.
∵菱形ABCD关于AC对称,M是AB边上的中点,
∴M′是AD的中点,
又∵N是BC边上的中点,
∴AM′∥BN,AM′=BN,
∴四边形ABNM′是平行四边形,
∴M′N=AB=2,
∴MP+NP=M′N=2,即MP+NP的最小值为2,
故选:C.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
电视机 | 电饭煲 | |
甲商店/元 | 100 | 60 |
乙商店/元 | 80 | 50 |
(1)设集团调配给甲商店x台电视机,则调配给甲商店电饭煲 台,调配给乙商店电视机 台、电饭煲 台;
(2)求出x的取值范围;
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.