题目内容
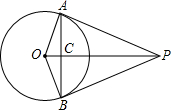 如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=
如图,PA,PB是⊙O的两条切线,切点分别为A,B,OP交AB于点C,OP=13,sin∠APC=| 5 | 13 |
(1)求⊙O的半径;
(2)求弦AB的长.
分析:(1)由题意可推出OA⊥AP,即可推出OA的长度,即半径的长度;
(2)根据题意和(1)的结论,即可推出PA=PB,∠APO=∠BPO,AC=BC=
AB,可以推出AC的长度,即可推出AB的长度.
(2)根据题意和(1)的结论,即可推出PA=PB,∠APO=∠BPO,AC=BC=
| 1 |
| 2 |
解答:解:(1)∵PA,PB是⊙O的两条切线,
∴∠OAP=90°,
∵sin∠APC=
=
,OP=13,
∴OA=5,
即所求半径为5.
(2)Rt△OAP中,AP=12,
∵PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO,
∴PC⊥AB
由S四边形OAPB=S△OAP+S△OBP,得
OP×AB=OA×AP,
∴AB=
=
.
∴∠OAP=90°,
∵sin∠APC=
| OA |
| OP |
| 5 |
| 13 |
∴OA=5,
即所求半径为5.
(2)Rt△OAP中,AP=12,
∵PA,PB是⊙O的两条切线,
∴PA=PB,∠APO=∠BPO,
∴PC⊥AB
由S四边形OAPB=S△OAP+S△OBP,得
| 1 |
| 2 |
∴AB=
| 2×5×12 |
| 13 |
| 120 |
| 13 |
点评:本题主要考查切线的性质、解直角三角形,解题的关键在于切线的性质找到直角三角形,然后解直角三角形.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
如图,PA,PB是⊙O的切线,切点分别为A,B,且∠APB=50°,点C是优弧
 如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度.
如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30度. 4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
4、如图,PA、PB是⊙O的两条切线,A、B是切点,连接AB,直线PO交AB于M.请你根据圆的对称性,写出△PAB的三个正确的结论.
 (2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于
(2012•谷城县模拟)如图,PA、PB是⊙O 的切线,切点分别是A、B,点C是⊙O上异与点A、B的点,如果∠P=60°,那么∠ACB等于