题目内容
【题目】如图，在四边形ABCD中，BA=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．
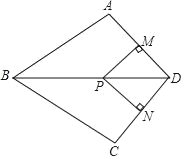
（1)求证：点A与C关于直线BD对称.
(2)若∠ADC=90°，求证四边形MPND为正方形.
【答案】见解析
【解析】
（1）首先根据角平分线的定义求出∠ABD=∠CBD，然后在△ABD和△CBD中，根据SAS证明两个三角形全等，进而得到∠ADB=∠CDB，AD=CD，根据等腰三角形的性质可得BD垂直平分AC，进而可得点A与C关于直线BD对称；
（2）首先证明四边形PMDN是矩形，再根据角平分线上的点到角两边的距离相等可得PM=PN，进而可得四边形MPND为正方形．
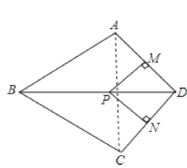
证明：(1)连接AC，
∵BD平分∠ABC，
∴∠ABD=∠CBD，
在△ABD和△CBD中
，
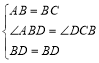∴△ABD≌△CBD(SAS)，
∴∠ADB=∠CDB，DA=DC，
∴BD垂直平分AC，
∴点A与C关于直线BD对称；
(2)∵PM⊥AD，PN⊥CD，
∴∠PMD=∠PND=90°，
∵∠ADC=90°，
∴四边形PMDN是矩形，
∵∠ADB=∠CDB，
∴BD平分∠ADC，
∵PM⊥AD，PN⊥CD，
∴PM=PN，
∴四边形MPND为正方形
名师指导期末冲刺卷系列答案【题目】某校准备在国庆节期间组织学生到泰山进行研学旅行，已知老师与学生一共25人参加此次研学旅行，购买门票共花费1700元，门票费用如表格所示，求参加研学旅行的老师和学生各有多少人？设老师有x人，学生有y人，则可列方程组为（ ）
景点 | 票价 | 开放时间 |
泰山门票 | 旺季：125元/人 淡季：100元/人 | 全天 |
说明：（1）旺季时间（2月～11月)，淡季时间（12月－次年1月）； （2）老年人（60岁～70岁）、学生、儿童（1.2米～1.4米）享受5折优惠； （3）教师、省部级劳模、英模、道德模范享受8折优惠； （4）现役军人、伤残军人、70岁以上老年人、残疾人，凭本人有效证件免费进山； （5）享受优惠的游客请出示本人有效证件。 | ||
A. 
B. 
C. 
D. 
【题目】观察理解，并解决问题.
问题情境：如图所示，用一些相同的小正方形，拼在一起，排成如下的一些大正方形：
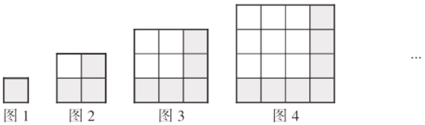
问题解决：（1）完成下表：
图序号 | 1 | 2 | 3 | 4 | … |
|
每一行小正方形的个数 | 1 | 2 | 3 | ______ | … | ______ |
阴影小正方形的个数 | 1 | 3 | 5 | ______ | … | ______ |
（2）根据图形规律推测：
______（用含
的代数式表示）
（3）像（1），（2）这样，根据某类事物的部分对象具有的某种性质，推出这类事物的所有对象具有的这种性质的推理，叫做归纳推理.对于科学的发现，归纳推理是十分有用的，通过观察、实验，对有限个对象的性质作归纳整理，提出对某类事物带有规律性的猜测，是科学研究的基本方法.请观察下列等式的规律：第一个等式：
；第二个等式：
；第三个等式：
；…猜想并直接写出第个等式.（用含的代数式表示）
