题目内容
【题目】
(1) 填空:AB=_________,BC= ;
(2) 若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.设运动时间为t秒,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,用含t的代数式表示BC和AB的长,并探索:BC-AB的值是否随着时间t的变化而改变?请说明理由
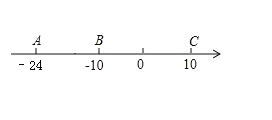
【答案】(1)、AB=14;BC=20;(2)、不变
【解析】试题分析:(1)、根据两点之间的距离公式求出AB和BC的长度;(2)、首先分别用含t的代数式表示A、B、C三点所表示的数,然后分别求出BC和AB的长度,然后进行计算.
试题解析:(1)、AB=﹣10﹣(﹣24)=14,BC=10﹣(﹣10)=20.
(2)、不变. ∵经过t秒后,A、B、C三点所对应的数分别是﹣24﹣t,﹣10+3t,10+7t,
∴BC=(10+7t)﹣(﹣10+3t)=4t+20, AB=(﹣10+3t)﹣(﹣24﹣t)=4t+14,
∴BC﹣AB=(4t+20)﹣(4t+14)=6. ∴BC﹣AB的值不会随着时间t的变化而改变.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目