Question

【题目】已知：如图，AB为⊙O的直径，点C、D在⊙O上，且BC=6cm，AC=8cm，∠ABD=45°．

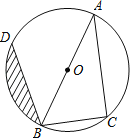
（1）求BD的长；

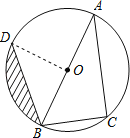
（2）求图中阴影部分的面积．

Answer 1

【答案】（1）BD=5cm．（2）S阴影= cm2．

【解析】

试题分析：（1）由AB为⊙O的直径，得到∠ACB=90°，由勾股定理求得AB，OB=5cm．连OD，得到等腰直角三角形，根据勾股定理即可得到结论；

（2）根据S阴影=S扇形﹣S△OBD即可得到结论．

解：（1）∵AB为⊙O的直径，

∴∠ACB=90°，

∵BC=6cm，AC=8cm，

∴AB=10cm．

∴OB=5cm．

连OD，

∵OD=OB，

∴∠ODB=∠ABD=45°．

∴∠BOD=90°．

∴BD==5cm．

（2）S阴影=S扇形﹣S△OBD=π52﹣×5×5=cm2．