题目内容
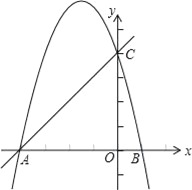
【题目】如图,抛物线y=ax2﹣bx﹣4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
(1)求抛物线的解析式,并用配方法把其化为y=a(x﹣h)2+k的形式,写出顶点坐标;
(2)已知点D(m,1﹣m)在第二象限的抛物线上,求出m的值,并直接写出点D关于直线AC的对称点E的坐标.
【答案】(1)此抛物线的解析式为y=﹣x2﹣3x+4. ![]() ;(-
;(-![]() ,
, ![]() );(2)m1=﹣3,m2=1.E(0,1).
);(2)m1=﹣3,m2=1.E(0,1).
【解析】试题分析:(1)由抛物线y=ax2+bx﹣4a经过A(1,0)、C(0,4)两点,利用待定系数法即可求得抛物线的解析式;
(2)由点D(m,1﹣m)在抛物线y=﹣x2﹣3x+4上,即可求得点D的坐标,则可求得∠CBO的度数,然后过点D作DF⊥BC于F,延长DE交y轴于E,又由点E即为点D关于直线BC的对称点,即可求得点E的坐标.
试题解析:(1)抛物线y=ax2+bx﹣4a经过A(1,0)、C(0,4)两点,
∴![]() ,
,
解得![]() .
.
∴此抛物线的解析式为y=﹣x2﹣3x+4.
(2)∵点D(m,1﹣m)在抛物线y=﹣x2﹣3x+4上,
∴﹣m2﹣3m+4=1﹣m,
解得m1=﹣3,m2=1.
∵点D在第二象限,
∴D(﹣3,4).
令y=﹣x2﹣3x+4=0,
解得x1=1,x2=﹣4.
∴B(﹣4,0).
∴∠CBO=45°.
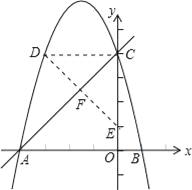
连接DC,
易知DC∥BA,DC⊥CO,DC=3.
∴∠DCA=∠CAO=45°.
∴∠ACD=45°.
过点D作DF⊥BC于F,延长DE交y轴于E,
∴∠D=45°.
∴∠CFE=45°.
∴DF=CF=EF.
∴点E即为点D关于直线BC的对称点.
∴CD=CE=3,
∴OE=1
∴E(0,1).

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目