题目内容
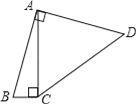
【题目】如图,在△ABC中,AB =AC=2,∠B = 40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE = 40°,DE交线段AC于点E.
(1)当∠BDA = 115°时,∠BAD= °,∠DEC = °,当点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”) .
(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.

【答案】(1)25,115,小;(2)当DC=2时,△ABD ≌△DCE,理由见解析;(3)存在.∠BDA=110°或80°.
【解析】试题分析:
(1)根据三角形的内角和计算∠BAD,再由三角形的一个外等于和它不相邻的两个内角的和求∠EDC,从而可得∠DEC,根据三角形的内角和判断∠BDA的大小变化.
(2)在(1)中可得到这两个三角形的三个角都相等,只要有一条边对应相等即可,而已知AB=2,所以CD=2.
(3)假设等腰△ADE存在,因为底边不确定,所以需要分三种情况讨论,求出∠BDA的度数后要检验.
试题解析:
(1)∠BAD=180°-∠B-∠BDA=180°-40°-115°=25°.
∵∠ADC=∠B+∠BAD,∴40°+∠EDC=40°+∠BAD,∴∠EDC=∠BAD.
∴∠DEC=180°-∠C-∠EDC=180°-40°-25°=115°.
∵在点D从点B向点C运动的过程中,对于△ABD,∠B=40°不变,∠BAD逐渐变大,
∴∠ADB逐渐变小.
(2)当DC=2时,△ABD≌△DCE,理由如下:
在△ABD和△DCE中,
因为∠B=∠C,∠BAD=∠CDE,已经有了两个角分别相等,所以只需要一边对应相等即可.
AB=AC=2,当DC=AB时,则可用ASA证明这两个三角形全等.
(3)在点D的运动过程中,存在△ADE是等腰三角形。理由如下:
①当DA=DE时,∠DAE=(180°-∠ADE)÷2=(180°-40°)÷2=70°.
所以∠BDA=∠C+∠DAE=40°+70°=110°.
②当AD=AE时,∠DAE=180°-2×40°=100°,
所以∠BDA=∠C+∠DAE=40°+100°=140°,
但∠BDA=180°-∠B-∠BAD=180°-40°-∠BAD,所以∠BDA<140°,
所以AD=AE不存在.
③当EA=ED时,∠DAE=∠EDA=40°,
所以∠BDA=∠DAE+∠C=40°+40°=80°.
综上所述,∠BDA=110°或80°.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
人 数 | 1 | 4 | 3 | 2 | 2 |
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.