题目内容
【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E。
(1)线段AB与DB的大小关系为 ,请证明你的结论;
(2)判断CE与⊥⊙O的位置关系,并证明;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明。

【答案】(1)AB=DB,理由见解析;(2)CE是⊙O的切线,理由见解析;(3)△ABD为等边三角形,理由见解析
【解析】试题分析:
(1)如图,连接BC,由AB是⊙O的直径可得:BC⊥AD,再由AC=CD,可得BC是AD的垂直平分线,从而由线段垂直平分线的性质可得AB=BD;

(2)如图,连接OC,由已知:OA=OB,AC=CD,可得OC是△ABD的中位线,从而得到OC∥BD,又∵CE⊥BD,可得CE⊥OC,就可得到CE是⊙O的切线;
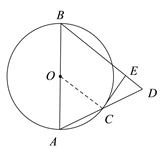
(3)如图,由已知S△CDE:S四边形ACEB=1:7易得S△CDE:S△ABD=1:8,连接BC,由AC=CD=![]() AD可得S△ABD=2S△BCD,∴S△CDE:2S△BCD=1:8,则S△CDE:S△BCD=1:4;由(1)和已知易证△BCD∽△CED,从而可得:
AD可得S△ABD=2S△BCD,∴S△CDE:2S△BCD=1:8,则S△CDE:S△BCD=1:4;由(1)和已知易证△BCD∽△CED,从而可得: ![]() ,∴
,∴![]() 即BD=2CD,再由AB=BD,AD=2BD,就可得到:AB=BD=AD,∴△ABD是等边三角形.
即BD=2CD,再由AB=BD,AD=2BD,就可得到:AB=BD=AD,∴△ABD是等边三角形.
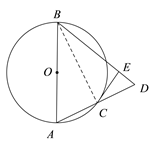
试题解析:
(1)线段AB=DB,
证明如下:
连结BC,∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AD.
又∵AC=CD,∴BC垂直平分线段AD,
∴AB=DB;
(2)CE是⊙O的切线.
证明如下:
连结OC.
∵点O为AB的中点,点C为AD的中点,
∴OC为△ABD的中位线,∴OC∥BD,
又∵CE⊥BD,∴CE⊥OC,∴CE是⊙O的切线;
(3)△ABD为等边三角形.
证明如下:
由![]() =
=![]() ,
,
得![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
, ![]() =
=![]() ,
,
∵∠D=∠D,∠CED=∠BCD=90°,∴△CED∽△BCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
在Rt△BCD中,∵CD=![]() BD,
BD,
∴∠CBD=30°,∴∠D=60°,又∵AB=DB,
∴△ABD为等边三角形.