题目内容
【题目】如图
(1)如图①,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
(2)如图②,已知在△ABC中,∠A=40°,剪去∠A后成四边形,∠1+∠2=;
(3)根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是;
(4)如图③,若没有剪掉∠A,而是把它折成如图所示的形状,试探究∠1+∠2与∠A的关系,并说明理由.
【答案】
(1)C
(2)220°
(3)∠1+∠2=180°+∠A
(4)解:∠1+∠2=2∠A.理由如下:
∵△EFP是由△EFA折叠得到的,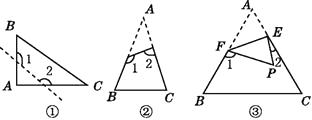
∴∠AFE=∠PFE,∠AEF=∠PEF.
∴∠1=180°-2∠AFE,∠2=180°-2∠AEF.
∴∠1+∠2=360°-2(∠AFE+∠AEF).
又∵∠AFE+∠AEF=180°-∠A,
∴∠1+∠2=360°-2(180°-∠A)=2∠A
【解析】解:(1)∵△ABC为直角三角形,
∴∠B+∠C=90°
∴∠1+∠2=360°-90°=270°
(2)∵△ABC中,∠A=40°,
∴∠B+∠C=180°-40°=140°,
∴∠1+∠2=360°-140°=220°(1)先根据三角形的内角和定理求出∠B+∠C的度数,再利用四边形的内角和定理得出∠B+∠C+∠1+∠2=360°,计算即可求出答案。
(2)先根据三角形的内角和定理求出∠B+∠C的度数,再利用四边形的内角和定理得出∠B+∠C+∠1+∠2=360°,计算即可求出答案。
(3)根据折叠的性质得出∠AFE=∠PFE,∠AEF=∠PEF,再根据平角的定义求出∠1=180°-2∠AFE,∠2=180°-2∠AEF,然后再求出∠1+∠2与∠A的关系即可。

【题目】下列调查中,适合用抽样调查的为_________(填序号).
①了解全班同学的视力情况;
②了解某地区中学生课外阅读的情况;
③了解某市百岁以上老人的健康情况;
④日光灯管厂要检测一批灯管的使用寿命.
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表(表1)和扇形统计图如下: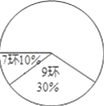
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.

