题目内容
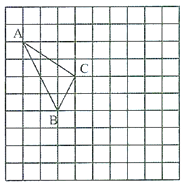
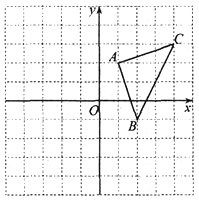
【题目】某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
【答案】解:如图作CM∥AB交AD于M,MN⊥AB于N.

由题意 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,CM=
,CM= ![]() ,
,
在RT△AMN中,∵∠ANM=90°,MN=BC=4,∠AMN=72°,
∴tan72°= ![]() ,
,
∴AN≈12.3,
∵MN∥BC,AB∥CM,
∴四边形MNBC是平行四边形,
∴BN=CM= ![]() ,
,
∴AB=AN+BN=13.8米.
【解析】作CM∥AB交AD于M,MN⊥AB于N.首先可证明△RPQ∽△DMC,依据相似三角形的性质可得到CM的长,然后在RT△AMN中依据锐角三角形函数的定义求得AN的长,最后依据AB=AN+BN求解即可.

练习册系列答案
相关题目
【题目】某超市的某种商品一周内每天的进价与售价信息和实际每天的销售量情况如图表所示:
进价与售价折线图(单位:元/斤)

实际销售量表(单位:斤)
日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
销售量 | 30 | 40 | 35 | 30 | 50 | 60 | 50 |
则下列推断不合理的是( )
A. 该商品周一的利润最小
B. 该商品周日的利润最大
C. 由一周中的该商品每天售价组成的这组数据的众数是4(元/斤)
D. 由一周中的该商品每天进价组成的这组数据的中位数是3(元/斤)