题目内容
我们给出如下定义:若一个四边形ABCD中AC⊥BD,BD平分AC,则称这个四边形为筝形四边形.
(1)小明说:“筝形四边形一定是菱形”.你认为小明的说法是否正确?若正确请说明理由;若不正确,请举个反例说明.
(3)在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,tan∠DAC=1.求证:筝形ABCD是正方形.
(1)小明说:“筝形四边形一定是菱形”.你认为小明的说法是否正确?若正确请说明理由;若不正确,请举个反例说明.
(3)在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,tan∠DAC=1.求证:筝形ABCD是正方形.
分析:(1)根据已知不能推出符合平行四边形的判定定理的条件,即得不出四边形ABCD是平行四边形,即不能得出四边形ABCD是菱形;
(2)先根据等腰三角形性质和三角形的内角和定理推出∠BAC=∠BCA=∠DAC=∠DCA,求出∠BAD=∠BCD,得出四边形ABCD是平行四边形,根据AB=BC,推出平行四边形ABCD是菱形,由tan∠DAC=1,求出∠DAC=45°,求出∠BAD=90°,根据正方形的判定推出即可.
(2)先根据等腰三角形性质和三角形的内角和定理推出∠BAC=∠BCA=∠DAC=∠DCA,求出∠BAD=∠BCD,得出四边形ABCD是平行四边形,根据AB=BC,推出平行四边形ABCD是菱形,由tan∠DAC=1,求出∠DAC=45°,求出∠BAD=90°,根据正方形的判定推出即可.
解答:(1)解:小明的说法不对:如图:
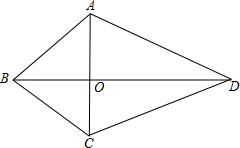
∵由已知BD平分AC和AC⊥BD不能推出OB=OD,
∴四边形ABCD不一定是平行四边形,
即筝形四边形不一定是菱形,
∴小明的说法不对.
(2)证明:∵AB=BC,AD=DC,
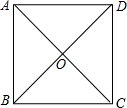
∴∠BAC=∠BCA,∠DAC=∠DCA,
∵∠ABC=∠ADC,∠ABC+∠BAC+∠BCA=180°,∠ADC+∠DAC+∠DCA=180°,
∴∠BAC=∠BCA=∠DAC=∠DCA,
∴∠BAC+∠DAC=∠BCA+∠DCA,
即∠BAD=∠BCD,
∵∠ABC=∠ADC,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形,
∵AC⊥BD,
∴∠AOD=90°,
∵tan∠DAC=1,
∴∠DAC=45°,
∴∠BAD=45°+45°=90°,
∴菱形ABCD是正方形.

∵由已知BD平分AC和AC⊥BD不能推出OB=OD,
∴四边形ABCD不一定是平行四边形,
即筝形四边形不一定是菱形,
∴小明的说法不对.
(2)证明:∵AB=BC,AD=DC,

∴∠BAC=∠BCA,∠DAC=∠DCA,
∵∠ABC=∠ADC,∠ABC+∠BAC+∠BCA=180°,∠ADC+∠DAC+∠DCA=180°,
∴∠BAC=∠BCA=∠DAC=∠DCA,
∴∠BAC+∠DAC=∠BCA+∠DCA,
即∠BAD=∠BCD,
∵∠ABC=∠ADC,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形,
∵AC⊥BD,
∴∠AOD=90°,
∵tan∠DAC=1,
∴∠DAC=45°,
∴∠BAD=45°+45°=90°,
∴菱形ABCD是正方形.
点评:本题考查了正方形、平行四边形、菱形、矩形的判定,三角形的内角和定理,等腰三角形的性质等知识点,主要考查学生综合运用定理进行推理的能力,题目综合性比较强,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 24、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
24、我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.