题目内容
24、我们给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称这个四边形为勾股四边形，这两条相邻的边称为这个四边形的勾股边．（1）写出你所学过的特殊四边形中是勾股四边形的两种图形的名称
矩形
，正方形
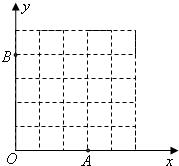
；（2）如图，已知格点（小正方形的顶点）O（0，0），A（3，0），B（0，4），请你画出以格点为顶点，OA，OB为勾股边且对角线相等的勾股四边形OAMB．
分析：（1）根据定义和特殊四边形的性质，则有矩形或正方形或直角梯形；
（2）根据要求和图形，分析知该四边形即为矩形，画图即可．
（2）根据要求和图形，分析知该四边形即为矩形，画图即可．
解答：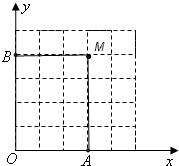
解：（1）矩形、正方形；
（2）根据要求和图形，则该四边形即为矩形，
根据上述定义可知只要有一个角为直角的四边形就是勾股四边形，
∵∠BOA为直角，∴点M在点（4，3）时四边形OAMB为勾股四边形，
∴点M横纵坐标分别为4，3，
由勾股定理知AM2+AO2=OM2
∴OM=5
∵由勾股定理得AB也为5，
∴对角线相等，
∴OA，OB为勾股边且对角线相等的勾股四边形OAMB 点M坐标还有（4，3）
．
解：（1）矩形、正方形；（2）根据要求和图形，则该四边形即为矩形，
根据上述定义可知只要有一个角为直角的四边形就是勾股四边形，
∵∠BOA为直角，∴点M在点（4，3）时四边形OAMB为勾股四边形，
∴点M横纵坐标分别为4，3，
由勾股定理知AM2+AO2=OM2
∴OM=5
∵由勾股定理得AB也为5，
∴对角线相等，
∴OA，OB为勾股边且对角线相等的勾股四边形OAMB 点M坐标还有（4，3）
．
点评：此题考查了学生对新定义的理解以及特殊四边形的性质．
练习册系列答案
新思维寒假作业系列答案
相关题目
