题目内容
【题目】已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,
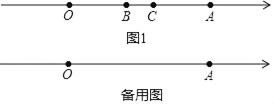
(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC﹣OB=![]() AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
【答案】(1)线段AC=OB,此时b的值是4;(2)若AC﹣OB=![]() AB,满足条件的b值是
AB,满足条件的b值是![]() 或﹣5.
或﹣5.
【解析】试题分析:(1)由题意可知B点表示的数比点C对应的数少3,进一步用b表示出AC、OB之间的距离,联立方程求得b的数值即可;
(2)分别用b表示出AC、OB、AB,进一步利用AC-0B=![]() AB建立方程求得答案即可.
AB建立方程求得答案即可.
试题解析:(1)由题意得:
11﹣(b+3)=b,
解得:b=4.
答:线段AC=OB,此时b的值是4.
(2)由题意得:
①11﹣(b+3)﹣b=![]() (11﹣b),
(11﹣b),
解得:b=![]() .
.
②11﹣(b+3)+b=![]() (11﹣b),
(11﹣b),
解得:b=﹣5.
答:若AC﹣OB=![]() AB,满足条件的b值是
AB,满足条件的b值是![]() 或﹣5.
或﹣5.

练习册系列答案
相关题目






