题目内容
【题目】点P、Q分别是边长为4cm的等边![]() 的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是
的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是![]() ,设运动时间为t秒.
,设运动时间为t秒.
![]() 连接AQ、CP交于点M,则在P、Q运动的过程中,
连接AQ、CP交于点M,则在P、Q运动的过程中,![]() 变化吗:若变化,则说明理由,若不变,则求出它的度数;
变化吗:若变化,则说明理由,若不变,则求出它的度数;
![]() 连接PQ,
连接PQ,
![]() 当
当![]() 秒时,判断
秒时,判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 当
当![]() 时,则
时,则![]() ______秒
______秒![]() 直接写出结果
直接写出结果![]()
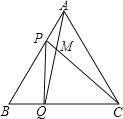
【答案】(1)在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;(2)①△BPQ是等边三角形;②![]() .
.
【解析】
(1)先证明△ABQ≌△CAP,得到∠BAQ=∠ACP,根据∠BAQ+∠QAC=60°,然后利用三角形外角的性质即可得出结论;
(2)①当t=2秒时,AP=BQ=2,PB=4﹣2=2,可知△BPQ是等边三角形;
②当PQ⊥BC时,∠B=60°,根据直角三角形30°所对直角边等于斜边一半的性质列等量关系,即可求出时间t.
(1)∵△ABC为等边三角形,
∴AB=AC,∠B=∠PAC=60°,
∵点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,
在△APC和△BQA中
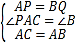 ,
,
∴△APC≌△BQA(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠CAQ+∠ACP=∠BAQ+∠CAQ=∠BAC=60°,
∴在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°;
故答案为:在P、Q运动的过程中,∠CMQ不变,∠CMQ=60°.
(2)①∵运动时间为ts,则AP=BQ=t,
∴PB=4﹣t,
当t=2秒时,AP=BQ=2,PB=4﹣2=2,∴AP=BQ=PB,
∴△BPQ是等边三角形;
故答案为:△BPQ是等边三角形.
②∵运动时间为ts,则AP=BQ=t,∴PB=4﹣t,
∵PQ⊥BC,∴∠PQB=90°,
∵∠B=60°,∴PB=2BQ,
∴4﹣t=2t,解得t=![]() ,
,
故答案为:t=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案