题目内容
【题目】如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为半径OH上一点,点E,F分别在矩形ABCD的边BC和CD上.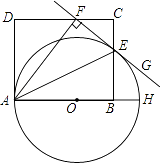
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
【答案】
(1)解:如图1,连接OE,
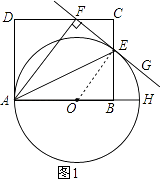
∵OA=OE,
∴∠EAO=∠AEO,
∵AE平分∠FAH,
∴∠EAO=∠FAE,
∴∠FAE=∠AEO,
∴AF∥OE,
∴∠AFE+∠OEF=180°,
∵AF⊥GF,
∴∠AFE=∠OEF=90°,
∴OE⊥GF,
∵点E在圆上,OE是半径,
∴GF是⊙O的切线
(2)解:∵四边形ABCD是矩形,CD=10,
∴AB=CD=10,∠ABE=90°,
设OA=OE=x,则OB=10﹣x,
在Rt△OBE中,∠OBE=90°,BE=5,
由勾股定理得:OB2+BE2=OE2,
∴(10﹣x)2+52=x2,
∴ ![]() ,
,
![]() ,
,
∴⊙O的直径为 ![]()
【解析】(1)根据OA=OE和AE平分∠FAH,易证得AF∥OE,再由FG⊥AF,从而证得OE⊥GF,即可得出结论。
(2)由四边形ABCD是矩形,可求出AB的长及∠ABE=90°,已知EB=5,因此连接OE,在Rt△OBE中,设圆的半径为x,可表示出OB的长,根据勾股定理即可求得圆的半径和直径。
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目