题目内容
 如图,∠AOC与∠BOC是邻补角,OD,OE分别是∠AOC,∠BOC的平分线.
如图,∠AOC与∠BOC是邻补角,OD,OE分别是∠AOC,∠BOC的平分线.(1)写出∠AOE的补角;
(2)若∠BOC=62°,求∠COD的值;
(3)试问射线OD与OE之间有什么特殊的位置关系?为什么?
分析:(1)根据补角的定义,即求与∠AOE的和是180°的角.由图易知∠AOE的补角有∠BOE,再由角平分线的定义,可知∠COE=∠BOE,从而得出∠AOE的补角是∠BOE与∠COE;
(2)首先根据邻补角的定义可知∠AOC=180°-∠BOC,得出∠AOC的度数,然后根据角平分线的定义得出∠COD=
∠AOC;
(3)根据角平分线及互为邻补角的定义,可求出∠DOE=90°,从而得出OD与OE之间的位置关系.
(2)首先根据邻补角的定义可知∠AOC=180°-∠BOC,得出∠AOC的度数,然后根据角平分线的定义得出∠COD=
| 1 |
| 2 |
(3)根据角平分线及互为邻补角的定义,可求出∠DOE=90°,从而得出OD与OE之间的位置关系.
解答:解:(1)∠AOE的补角是∠BOE与∠COE;
(2)∵∠AOC=180°-∠BOC=180°-62°=118°,
又∵OD是∠AOC的平分线,
∴∠COD=
∠AOC=
×118°=59°;
(3)射线OD与OE互相垂直.理由如下:
∵OD是∠AOC的平分线,∴∠COD=
∠AOC,
∵OE是∠BOC的平分线,∴∠COE=
∠BOC.
∵∠AOC+∠BOC=180°,
∠AOC+
∠BOC=90°,
∴∠COD+∠COE=90°,∴∠DOE=90°.
∴OD⊥OE.
(2)∵∠AOC=180°-∠BOC=180°-62°=118°,
又∵OD是∠AOC的平分线,
∴∠COD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)射线OD与OE互相垂直.理由如下:
∵OD是∠AOC的平分线,∴∠COD=
| 1 |
| 2 |
∵OE是∠BOC的平分线,∴∠COE=
| 1 |
| 2 |
∵∠AOC+∠BOC=180°,
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COD+∠COE=90°,∴∠DOE=90°.
∴OD⊥OE.
点评:此题综合考查角平分线,邻补角,补角,垂直的定义及角度的简单计算.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 17、如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,求∠AOB的度数.
17、如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,求∠AOB的度数.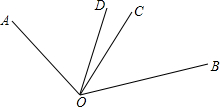 如图,∠AOC与∠BOC的度数之比是5﹕3,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.
如图,∠AOC与∠BOC的度数之比是5﹕3,OD平分∠AOB,若∠COD=15°,求∠AOB的度数. 如图,∠AOC与∠COB互为邻补角,OD,OE分别是∠AOC和∠BOC的平分线,则∠DOE=
如图,∠AOC与∠COB互为邻补角,OD,OE分别是∠AOC和∠BOC的平分线,则∠DOE= 如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )
如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )