题目内容
 如图,∠AOC与∠COB互为邻补角,OD,OE分别是∠AOC和∠BOC的平分线,则∠DOE=
如图,∠AOC与∠COB互为邻补角,OD,OE分别是∠AOC和∠BOC的平分线,则∠DOE=90°
90°
.分析:根据角平分线的性质可得∠DOC=
∠AOC,∠COE=
∠COB,再根据邻补角互补可得∠AOC+∠BOC=180°,进而得到答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OD,OE分别是∠AOC和∠BOC的平分线,
∴∠DOC=
∠AOC,∠COE=
∠COB,
∵∠AOC+∠BOC=180°,
∴∠DOC=
∠AOC+
∠BOC=
×180°=90°,
故答案为:90°.
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOC+∠BOC=180°,
∴∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:90°.
点评:此题主要考查了邻补角和角平分线定义,关键是掌握角平分线的定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,∠AOC与∠BOC是邻补角,OD,OE分别是∠AOC,∠BOC的平分线.
如图,∠AOC与∠BOC是邻补角,OD,OE分别是∠AOC,∠BOC的平分线. 17、如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,求∠AOB的度数.
17、如图,∠AOC与∠BOD都是直角,且∠AOB:∠AOD=2:7,求∠AOB的度数.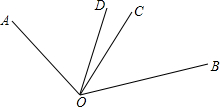 如图,∠AOC与∠BOC的度数之比是5﹕3,OD平分∠AOB,若∠COD=15°,求∠AOB的度数.
如图,∠AOC与∠BOC的度数之比是5﹕3,OD平分∠AOB,若∠COD=15°,求∠AOB的度数. 如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )
如图,∠AOC与∠BOD都是直角,且射线OB平分∠AOC,∠DOA的度数等于( )