题目内容
已知:四边形ABCD中,AB∥CD,且AB、CD的长是关于x的方程x2-2mx+(m-| 1 |
| 2 |
| 7 |
| 4 |
(1)当m=2和m>2时,四边形ABCD分别是哪种四边形并说明理由.
(2)若M、N分别是AD、BC的中点,线段MN分别交AC、BD于点P、Q,PQ=1,且AB<CD,求AB、CD的长;
(3)在(2)的条件下,AD=BC=2,求一个一元二次方程,使它的两个根分别是tan∠BDC和tan∠BCD.
分析:(1)根据当m=2和m>2时,方程根的情况来进一步判断AB和CD的数量关系,结合其位置关系,判断该四边形的形状;
(2)根据梯形的对角线的中点所连接的线段等于上下底差的一半,结合根与系数的关系得到关于m的方程,从而求出方程的两个根;
(3)根据梯形的边之间的关系,求得这两个角的度数,再根据特殊角的锐角三角函数值写出这个一元二次方程.
(2)根据梯形的对角线的中点所连接的线段等于上下底差的一半,结合根与系数的关系得到关于m的方程,从而求出方程的两个根;
(3)根据梯形的边之间的关系,求得这两个角的度数,再根据特殊角的锐角三角函数值写出这个一元二次方程.
解答:解:(1)当m=2时,x2-4x+4=0.
∵△=0,方程有两个相等的实数根.
∴AB=CD,此时AB∥CD,则该四边形是平行四边形;
当m>2时,△=m-2>0,
又∵AB+CD=2m>0,
AB•CD=(m-
)2+
>0,
∴AB≠CD.
该四边形是梯形.
(2)根据三角形的中位线定理可以证明:连接梯形的两条对角线的中点的线段等于梯形的上下底的差的一半.
则根据PQ=1,得CD-AB=2.
根据(1)中的AB+CD和AB•CD的式子得(2m)2-4(m2-m+2)=4,
∴m=3.
当m=3时,则有x2-6x+8=0,
∴x=2或x=4,
即AB=2,CD=4.
(3)根据该梯形是等腰梯形,平移一腰,则得到等边△BEC.
∴∠BCD=60°,∠BDC=30°.
∵tan∠BDC+tan∠BCD=
,
tan∠BDC•tan∠BCD=1.
∴所求作的方程是y2-
y+1=0.
∵△=0,方程有两个相等的实数根.
∴AB=CD,此时AB∥CD,则该四边形是平行四边形;
当m>2时,△=m-2>0,
又∵AB+CD=2m>0,
AB•CD=(m-
| 1 |
| 2 |
| 7 |
| 4 |
∴AB≠CD.
该四边形是梯形.
(2)根据三角形的中位线定理可以证明:连接梯形的两条对角线的中点的线段等于梯形的上下底的差的一半.
则根据PQ=1,得CD-AB=2.
根据(1)中的AB+CD和AB•CD的式子得(2m)2-4(m2-m+2)=4,
∴m=3.
当m=3时,则有x2-6x+8=0,
∴x=2或x=4,
即AB=2,CD=4.
(3)根据该梯形是等腰梯形,平移一腰,则得到等边△BEC.
∴∠BCD=60°,∠BDC=30°.
∵tan∠BDC+tan∠BCD=
| 4 |
| 3 |
| 3 |
tan∠BDC•tan∠BCD=1.
∴所求作的方程是y2-
| 4 |
| 3 |
| 3 |
点评:注意平行四边形的梯形的概念的区别;能够证明梯形的对角线中点所连线段等于上下底差的一半;能够根据根与系数的关系由已知方程写出两根之和,两根之积.反过来能够根据两根之和,两根之积写出一个方程.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
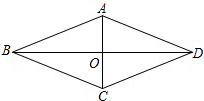 如图,已知,四边形ABCD是菱形,AC=6,BD=8,求AB的长和菱形ABCD的面积.
如图,已知,四边形ABCD是菱形,AC=6,BD=8,求AB的长和菱形ABCD的面积.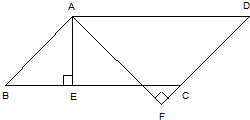 34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.
34、如图:在平行四边形ABCD中,∠B=30°,AE⊥BC于点E,AF⊥DC的延长线于点F,已知平行四边形ABCD的周长为40cm,且AE:AF=2:3.求平行四边形ABCD的面积.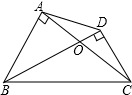 如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD.
如图,已知在四边形ABCD中,AC与BD相交于点O,AB⊥AC,CD⊥BD. 如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量
如图,已知平行四边形ABCD,E是边AB的中点,联结AC、DE交于点O.记向量