题目内容
【题目】如图，∠AOC：∠COD：∠BOD=2：3：4，且A，O，B三点在一条直线上，OE，OF分别平分∠AOC和∠BOD，OG平分∠EOF，求∠GOF的度数。
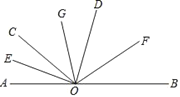
【答案】60°
【解析】
根据∠AOC：∠COD：∠BOD=2：3：4分别设∠AOC=2x，∠COD=3x，∠BOD=4x，根据这三个角之和等于180°，求得三个角的度数，然后根据角平分线的性质即可求得∠EOF的大小．
设∠AOC=2x，∠COD=3x，∠BOD=4x
∵∠AOC+∠COD+∠BOD=∠AOB=180°
∴2x+3x+4x=180°
∴x=20°
∴∠AOC=40°∠COD=60°∠BOD=80°
∵OE,OF平分∠AOC，∠BOD
∴∠EOC=20°，∠DOF=40°
∴∠EOF=120°
又∵OG平分∠EOF
∴∠EOG=∠GOF=60°
∴∠GOF=60°.
练习册系列答案
优质课堂快乐成长系列答案
相关题目
