题目内容
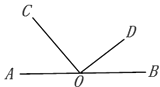
【题目】如图, EF∥AD, AD∥BC, CE平分 ![]() ,
, ![]() .求
.求 ![]() 的度数.
的度数.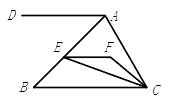
【答案】解:∵AD∥BC,
∴∠DAC+∠ACB=180°,
∵∠DAC=120°,
∴∠ACB=60°,
∵∠ACF=20°,
∴∠BCF的=40°,
∵CE平分∠BCF,
∴∠BCE=∠ECF=20°,
∵EF∥AD,
∴EF∥BC,
∴∠FEC=∠BCE=20°.
【解析】根据AD∥BC,∠DAC+∠ACB=180°,再由∠DAC=120°,得出∠ACB=60°,由∠ACF=20°,得∠BCF的度数,根据CE平分∠BCF,得∠BCE=∠ECF,因为EF∥AD,则EF∥BC,∠FEC=∠BCE,即可得出∠FEC=∠FCE.
【考点精析】本题主要考查了角的平分线和平行线的性质的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能正确解答此题.

练习册系列答案
相关题目