��Ŀ����
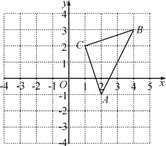
����Ŀ����1����ͼ�٣��ı��� ABCD �������Σ��� G �� BC �ϵ�����һ�㣬BF AG �ڵ� F��DE AG�ڵ� E��̽�� BF��DE��EF ֮���������ϵ����һѧϰС�����̽���õ�DE�CBF= EF����֤��������ۣ�
��2������1���еĵ� G �� CB ���ӳ����ϣ������������䣬����ͼ���л���ͼ�Σ���ֱ��д����ʱ BF��DE��EF ֮���������ϵ��
��3����ͼ �� ���ı��� ABCD �ڽ��� ��O��AB=AD��E ��F ��AC �ϵ����㣬�������AED=��BFA=��BCD�����ж� AC��DE��BF ֮���������ϵ����˵�����ɣ�

���𰸡���1��֤������������2��EF=BF+DE����3��AC=BF+DE��֤��������
����������1����������ABCD��BF��AG��DE��AG
�� AB=AD��
��BAF+��DAE=��BAF+��ABF=��AFB=��DEA=900
���DAE=��ABF
���ADE�ա�BAF
��BF=AE��AF=DE
�� EF= AF �CAE = DE�C BF

��2����ͼ��ͼ��ʾ

EF=BF+DE
��3���� �ı���ABCD�ڽ���Բ
�� ��BCD+��BAD=1800
�� ��AED=��BCD����AED+��DEC=1800
���BAD=��DEC
�� ��BAD=��1+��2����DEC=��1+��3
���2=��3
�ߡ�AED=��BFA��AB=AD
�� ��ADE�ա�BAF
�� AE=BF��DE=AF
����BD
�ߡ�AED=��BCD����1=��DBC
���3=��4
���ADB=��EDC
��AB=AD
���ADB=��ABD=��ACD
�� ��EDC=��ACD
�� DE=CE=AF
�� AC=AE+CE=BF+DE


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�