Question

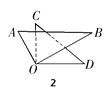
【题目】把一副三角尺的直角顶点O重叠在一起．

（1）如图1，若OC平分∠AOB，请猜想此时OB是不是平分∠COD？答：_________(只回答“是”或“不是”即可)

（2）如图21－2，若∠COB=∠1，OB在∠COD的内部，请你猜想∠AOC与∠DOB是否相等，并简述理由；

（3）在（2）的条件下，请问∠COB与∠AOD的和是多少？并简述理由.

Answer 1

【答案】(1)是;(2)∠AOC=∠DOB,理由见解析;(3)∠COB+∠AOD =180°, 理由见解析.

【解析】试题分析：（1）是，首先根据直角三角板的特点得到∠AOB=90°，∠COD=90°，再根据角平分线的定义计算出∠COB和∠BOD的度数即可；

（2）∠AOC与∠BOD相等；根据等角的余角相等即可得到答案；

（3）根据角的和差关系进行等量代换即可．

试题解析：解：（1）是．∵∠AOB=90°，OC恰好是∠AOB的角平分线，∴∠COB=45°，∵∠COD=90°，∴∠BOD=90°﹣45°=45°，∴∠COB=∠BOD，∴此时OB是∠COD的角平分线；

（2）∠AOC与∠BOD相等．∵∠AOB=∠COD=90°，∠COB=∠1，∴∠AOC=90°﹣∠1，∠BOD=90°﹣∠1，∴∠AOC=∠BOD；

（3）∠COB+∠AOD=180°．理由如下：

∠COB+∠AOD=∠COB+∠AOC+∠COD=∠AOB+∠DOC=90°+90°=180°．