题目内容
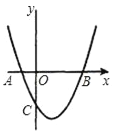
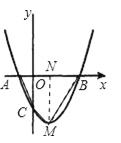
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点,与y轴交于点C.
(1)点A的坐标为 ,点B的坐标为 ,点C的坐标为 .
(2)设抛物线y=x2﹣2x﹣3的顶点为M,求四边形ABMC的面积.
【答案】(1)A(﹣1,0),B(3,0),C(0,﹣3);(2)9.
【解析】
试题分析:(1)把y=0和x=0分别代入解析式即可求出A、B、C的坐标;
(2)把解析式化成顶点式即可求出M的坐标,过M作MN⊥X轴于N,这样四边形ACMB的面积就转化成△ACO、梯形OCMN、△BMN的面积,根据点的坐标求出各个面积代入即可.
试题解析:(1)当y=0时,x2﹣2x﹣3=0,解得:x1=3,x2=﹣1,∴点A的坐标是(﹣1,0),点B的坐标是(3,0),当x=0时,y=﹣3,∴点C的坐标是(0,﹣3),故答案为:A(﹣1,0),B(3,0),C(0,﹣3);
(2)解:y=x2﹣2x﹣3=(x﹣1)2﹣4,∴M(1,﹣4),过M作MN⊥X轴于N,则:ON=1,MN=4,BN=3﹣1=2,OA=1,OC=3,∴四边形ABMC的面积S=S△COA+S梯形CONM+S△BNM=![]() OA×OC+
OA×OC+![]() ×(OC+MN)×ON+
×(OC+MN)×ON+![]() ×MN×BN=
×MN×BN=![]() ×1×3+
×1×3+![]() ×(3+4)×1+
×(3+4)×1+![]() ×2×4=9.
×2×4=9.
答:四边形ABMC的面积是9.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目