题目内容
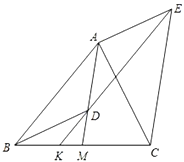
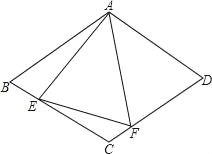
【题目】如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形的边BC,CD上.
(1)证明:BE=CF.
(2)当点E,F分别在边BC,CD上移动时(△AEF保持为正三角形),请探究四边形AECF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
(3)在(2)的情况下,请探究△CEF的面积是否发生变化?若不变,求出这个定值;如果变化,求出其最大值.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】试题分析:(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;
(3)当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF-S△AEF,则△CEF的面积就会最大.
试题解析:(1)证明:连接AC,
∵∠1+∠2=60°,∠3+∠2=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=∠ADC=60°
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴△ABC、△ACD为等边三角形
∴∠4=60°,AC=AB,
∴在△ABE和△ACF中,
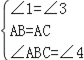 ,
,
∴△ABE≌△ACF.(ASA)
∴BE=CF.
(2)解:由(1)得△ABE≌△ACF,
则S△ABE=S△ACF.
故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
是定值.
作AH⊥BC于H点,
则BH=2,
S四边形AECF=S△ABC
=![]()
=![]()
=![]() ;
;
(3)解:由“垂线段最短”可知,
当正三角形AEF的边AE与BC垂直时,边AE最短.
故△AEF的面积会随着AE的变化而变化,且当AE最短时,
正三角形AEF的面积会最小,
又S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.
由(2)得,S△CEF=S四边形AECF﹣S△AEF
=![]() ﹣
﹣![]() =
=![]() .
.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案