题目内容
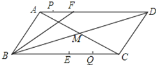
【题目】如图,![]() 中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
中,点E是BC的中点,点F在AD上,AF=6cm,BF=12cm,BD平分∠FBC,若点P,Q分别是AF,BC上点,且CQ=2AP.若点P、Q、E、F为顶点的四边形构成平行四边形,则AP的长为______.
【答案】3或5
【解析】
由四边形ABCD是平行四边形得出:AD∥BC,AD=BC,∠ADB=∠CBD,又由∠FBM=∠CBM,即可证得FB=FD,求出AD的长,得出CE的长,设AP=x,点P、Q、E、F为顶点的四边形是平行四边形,根据题意列出方程并解方程即可得出结果.
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∵∠FBM=∠CBM,
∴∠FBD=∠FDB,
∴FB=FD=12cm,
∵AF=6cm,
∴AD=18cm,
∵点E是BC的中点,
∴CE=![]() BC=
BC=![]() AD=9cm,
AD=9cm,
要使点P、Q、E、F为顶点的四边形是平行四边形,则PF=EQ即可,
设AP=x,则CQ=2AP=2x,
∵点P、Q、E、F为顶点的四边形是平行四边形,
根据题意得:6-x=9-2x或6-x=2x-9,
解得:x=3或x=5.
故答案为:3或5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某自行车厂一周计划生产![]() 辆自行车,平均每天生产
辆自行车,平均每天生产![]() 辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产________辆;
根据记录可知前三天共生产________辆;
![]() 产量最多的一天比产量最少的一天多生产________辆;
产量最多的一天比产量最少的一天多生产________辆;
![]() 该厂实行计件工资制,每辆车
该厂实行计件工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?