Question

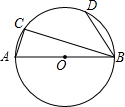
已知：如图，直径为OA的⊙M与x轴交于点O、A，点B、C把

OA

分为三等份，连接MC并延长交y轴于点D（0，3）
（1）求证：△OMD≌△BAO；
（2）若直线l：y=kx+b把⊙M的面积分为二等份，求证：

3

k+b=0．

Answer 1

证明：（1）连接BM，∵B、C把

OA

三等分，∴∠1=∠5=60°，1分
又∵OM=BM，∴∠2=

1

2

∠5=30°，2分
又∵OA为⊙M直径，∴∠ABO=90°，∴AB=

1

2

OA=OM，∠3=60°，3分
∴∠1=∠3，∠DOM=∠ABO=90°，4分
在△OMD和△BAO中，

∠1=∠3 OM=AB ∠DOM=∠ABO

5分
∴△OMD≌△BAO（ASA）．6分

（2）若直线l把⊙M的面积分为二等份，
则直线l必过圆心M，7分
∵D（0，3），∠1=60°，
∴OM=

OD

tan60°

=

3

3

=

3

，
∴M(

3

，0)，8分
把M（

3

，0）代入y=kx+b得：

3

k+b=0．