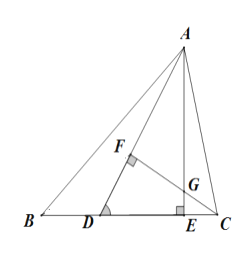
题目内容
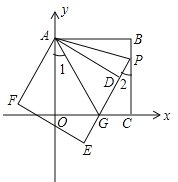
【题目】如图,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先求出![]() ,根据30°所对的直角边是斜边的一半,可得
,根据30°所对的直角边是斜边的一半,可得![]() ,从而得出
,从而得出![]() ,然后根据等边对等角可得
,然后根据等边对等角可得![]() ,然后利用外角的性质和等角对等边可证出
,然后利用外角的性质和等角对等边可证出![]() ,再利用等角对等边可得
,再利用等角对等边可得![]() ,从而得出
,从而得出![]() ,最后利用ASA即可证出
,最后利用ASA即可证出![]() ;
;
(2)先根据已知条件即可求出BD和CD,从而求出DF,再根据全等三角形的性质即可求出FC和FG,从而求出CG,最后根据30°所对的直角边是斜边的一半即可求出![]() .
.
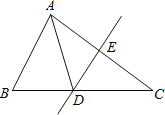
(1)证明:连接![]() ,
,
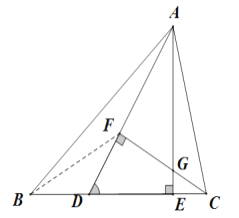
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
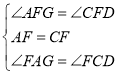
∴![]() ;
;
解:(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
【题目】今年3月,某集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩 | 评定等级 | 频数 |
| A | 2 |
| B | b |
| C | 15 |
| D | 6 |
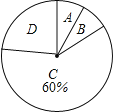
根据以上信息解答下列问题:
(1)求m,b的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;
(3)从评估成绩不少于80分的连锁店中,任选2家介绍营销经验,用树状图或列表法求其中至少有一家是A等级的概率.