题目内容
(2013•达州)选取二次三项式ax2+bx+c(a≠0)中的两项,配成完全平方式的过程叫配方.例如
①选取二次项和一次项配方:x2-4x+2=(x-2)2-2;
②选取二次项和常数项配方:x2-4x+2=(x-
)2+(2
-4)x,或x2-4x+2=(x+
)2-(4+2
)x
③选取一次项和常数项配方:x2-4x+2=(
x-
)2-x2
根据上述材料,解决下面问题:
(1)写出x2-8x+4的两种不同形式的配方;
(2)已知x2+y2+xy-3y+3=0,求xy的值.
①选取二次项和一次项配方:x2-4x+2=(x-2)2-2;
②选取二次项和常数项配方:x2-4x+2=(x-
| 2 |
| 2 |
| 2 |
| 2 |
③选取一次项和常数项配方:x2-4x+2=(
| 2 |
| 2 |
根据上述材料,解决下面问题:
(1)写出x2-8x+4的两种不同形式的配方;
(2)已知x2+y2+xy-3y+3=0,求xy的值.
分析:(1)根据配方法的步骤根据二次项系数为1,常数项是一次项系数的一半的平方进行配方和二次项和常数项在一起进行配方即可.
(2)根据配方法的步骤把x2+y2+xy-3y+3=0变形为(x+
y)2+
(y-2)2=0,再根据x+
y=0,y-2=0,求出x,y的值,即可得出答案.
(2)根据配方法的步骤把x2+y2+xy-3y+3=0变形为(x+
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
解答:解:(1)x2-8x+4
=x2-8x+16-16+4
=(x-4)2-12;
x2-8x+4
=(x-2)2+4x-8x
=(x-2)2-4x;
(2)x2+y2+xy-3y+3=0,
(x+
y)2+
(y-2)2=0,
x+
y=0,y-2=0,
x=-1,y=2,
则xy=(-1)2=1;
=x2-8x+16-16+4
=(x-4)2-12;
x2-8x+4
=(x-2)2+4x-8x
=(x-2)2-4x;
(2)x2+y2+xy-3y+3=0,
(x+
| 1 |
| 2 |
| 3 |
| 4 |
x+
| 1 |
| 2 |
x=-1,y=2,
则xy=(-1)2=1;
点评:本题考查了配方法的应用,根据配方法的步骤和完全平方公式:a2±2ab+b2=(a±b)2进行配方是解题的关键,是一道基础题.

练习册系列答案
相关题目
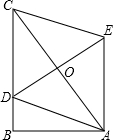 (2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )
(2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )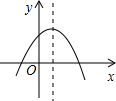 (2013•达州)二次函数y=ax2+bx+c的图象如图所示,反比例函数
(2013•达州)二次函数y=ax2+bx+c的图象如图所示,反比例函数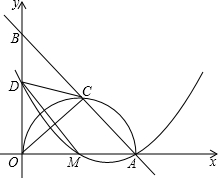 (2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.
(2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.