题目内容
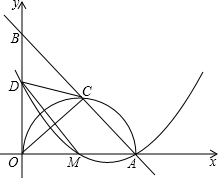 (2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.
(2013•达州)如图,在平面直角坐标系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3.取BO的中点D,连接CD、MD和OC.(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使S△QAM=
| 1 | 6 |
分析:(1)连接CM,可以得出CM=OM,就有∠MOC=∠MCO,由OA为直径,就有∠ACO=90°,D为OB的中点,就有CD=OD,∠DOC=∠DCO,由∠DOC+∠MOC=90°就可以得出∠DCO+∠MCO=90°而得出结论;
(2)根据条件可以得出△ACO∽△AOB而求出
=
,从而求出AB,在Rt△AOB中由勾股定理就可以求出OB的值,根据D是OB的中点就可以求出D的坐标,由待定系数法就可以求出抛物线的解析式,求出对称轴,根据轴对称的性质连接AD交对称轴于P,先求出AD的解析式就可以求出P的坐标;
(3)根据S△PDM=S△ADM-S△APM而求出其值就可以表示出S△QAM的大小,设Q的坐标为m,根据三角形的面积公式就可以求出横坐标而得出结论.
(2)根据条件可以得出△ACO∽△AOB而求出
| AC |
| AO |
| AO |
| AB |
(3)根据S△PDM=S△ADM-S△APM而求出其值就可以表示出S△QAM的大小,设Q的坐标为m,根据三角形的面积公式就可以求出横坐标而得出结论.
解答:(1)证明:连接CM,
∵AO是直径,M是圆心,
∴CM=OM,∠ACO=90°,
∴∠MOC=∠MCO.
∵D为OB的中点,
∴CD=OD,
∴∠DOC=∠DCO.
∵∠DOC+∠MOC=90°,
∴∠DCO+∠MCO=90°,
即∠MCD=90°,
∴CD是⊙M的切线;
(2)解:∵∠ACO=∠AOB=90°,∠OAB=∠OAB,
∴△ACO∽△AOB,
∴
=
,
∴
=
,
∴AB=
.
在Rt△AOB中,由勾股定理,得
BO=
,
∵D为OB的中点,
∴OD=
OB=
,
∴D(0,
).
∵OM=AM=
OA=
,
∴M(
,0).设抛物线的解析式为y=a(x-
)(x-5),由题意,得
=a(0-
)(0-5),
解得:a=
,
∴抛物线的解析式为:y=
(x-
)(x-5),
=
(x-
)2-
.
连接AD交对称轴于P,设直线AD的解析式为y=kx+b,由题意,得
,
解得:
,
∴直线AD的解析式为:y=-
x+
,
当x=
时,
y=
,
∴P(
,
);
(3)解:存在.
∵S△PDM=S△ADM-S△APM,
∴S△PDM=
×
×
-
×
×
,
=
,
∴S△QAM=
×
=
.
设Q的横坐标为m,由题意,得
×
|m|=
,
∴|m|=
,
∴m=±
,
当m=
时,
=
(x-
)2-
.
x1=
,x2=
,
当m=-
时,
-
=
(x-
)2-
.
x=
.
∴Q(
,
),(
,
),(
,-
).
∵AO是直径,M是圆心,
∴CM=OM,∠ACO=90°,
∴∠MOC=∠MCO.
∵D为OB的中点,
∴CD=OD,
∴∠DOC=∠DCO.
∵∠DOC+∠MOC=90°,
∴∠DCO+∠MCO=90°,
即∠MCD=90°,
∴CD是⊙M的切线;
(2)解:∵∠ACO=∠AOB=90°,∠OAB=∠OAB,
∴△ACO∽△AOB,
∴
| AC |
| AO |
| AO |
| AB |
∴
| 3 |
| 5 |
| 5 |
| AB |
∴AB=
| 25 |
| 3 |
在Rt△AOB中,由勾股定理,得
BO=
| 20 |
| 3 |
∵D为OB的中点,
∴OD=
| 1 |
| 2 |
| 10 |
| 3 |
∴D(0,
| 10 |
| 3 |
∵OM=AM=
| 1 |
| 2 |
| 5 |
| 2 |
∴M(
| 5 |
| 2 |
| 5 |
| 2 |
| 10 |
| 3 |
| 5 |
| 2 |
解得:a=
| 4 |
| 15 |
∴抛物线的解析式为:y=
| 4 |
| 15 |
| 5 |
| 2 |
=
| 4 |
| 15 |
| 15 |
| 4 |
| 5 |
| 12 |
连接AD交对称轴于P,设直线AD的解析式为y=kx+b,由题意,得
|
解得:
|
∴直线AD的解析式为:y=-
| 2 |
| 3 |
| 10 |
| 3 |
当x=
| 15 |
| 4 |
y=
| 5 |
| 6 |
∴P(
| 15 |
| 4 |
| 5 |
| 6 |
(3)解:存在.
∵S△PDM=S△ADM-S△APM,
∴S△PDM=
| 1 |
| 2 |
| 5 |
| 2 |
| 10 |
| 3 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 6 |
=
| 25 |
| 8 |
∴S△QAM=
| 25 |
| 8 |
| 1 |
| 6 |
| 25 |
| 48 |
设Q的横坐标为m,由题意,得
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 48 |
∴|m|=
| 5 |
| 12 |

∴m=±
| 5 |
| 12 |
当m=
| 5 |
| 12 |
| 5 |
| 12 |
| 4 |
| 15 |
| 15 |
| 4 |
| 5 |
| 12 |
x1=
15+5
| ||
| 4 |
15-5
| ||
| 4 |
当m=-
| 5 |
| 12 |
-
| 5 |
| 12 |
| 4 |
| 15 |
| 15 |
| 4 |
| 5 |
| 12 |
x=
| 15 |
| 4 |
∴Q(
15+5
| ||
| 4 |
| 5 |
| 12 |
15-5
| ||
| 4 |
| 5 |
| 12 |
| 15 |
| 4 |
| 5 |
| 12 |
点评:本题考查圆周角定理的运用,勾股定理的运用,圆的切线的判定定理的运用,待定系数法求函数的解析式的运用,抛物线的顶点式的运用,三角形的面积公式的运用,轴对称性质的运用,解答时求出抛物线的解析式是解答本题的关键.

练习册系列答案
相关题目
 (2013•达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=
(2013•达州)如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600米,E为弧CD上一点,且OE⊥CD,垂足为F,OF=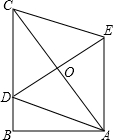 (2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( )
(2013•达州)如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D在BC上,以AC为对角线的所有?ADCE中,DE最小的值是( ) (2013•达州)如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是
(2013•达州)如图,折叠矩形纸片ABCD,使B点落在AD上一点E处,折痕的两端点分别在AB、BC上(含端点),且AB=6,BC=10.设AE=x,则x的取值范围是 (2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=
(2013•达州)如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2012BC和∠A2012CD的平分线交于点A2013,则∠A2013=