Question

【题目】已知A（1，0）、B（0，﹣1）、C（﹣1，2）、D（2，﹣1）、E（4，2）五个点，抛物线y=a（x﹣1）2+k（a＞0）经过其中的三个点．
（1）求证：C、E两点不可能同时在抛物线y=a（x﹣1）2+k（a＞0）上；
（2）点A在抛物线y=a（x﹣1）2+k（a＞0）上吗？为什么？
（3）求a和k的值．

Answer 1

【答案】
（1）解：∵抛物线y=a（x﹣1）2+k的对称轴为x=1，

而C（﹣1，2），E（4，2）两点纵坐标相等，

由抛物线的对称性可知，C、E关于直线x=1对称，

又∵C（﹣1，2）与对称轴相距2，E（4，2）与对称轴相距3，

∴C、E两点不可能同时在抛物线上

（2）解：假设点A（1，0）在抛物线y=a（x﹣1）2+k（a＞0）上，

则a（1﹣1）2+k=0，解得k=0，

因为抛物线经过5个点中的三个点，

将B（0，﹣1）、C（﹣1，2）、D（2，﹣1）、E（4，2）代入，

得出a的值分别为a=﹣1，a= ，a=﹣1，a= ，

所以抛物线经过的点是B，D，

又因为a＞0，与a=﹣1矛盾，

所以假设不成立．

所以A不在抛物线上

（3）解：将D（2，﹣1）、C（﹣1，2）两点坐标代入y=a（x﹣1）2+k中，得

，

解得 ，

或将E、D两点坐标代入y=a（x﹣1）2+k中，得

，

解得 ，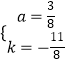

综上所述， 或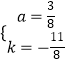

【解析】（1）由抛物线y=a（x﹣1）2+k可知，抛物线对称轴为x=1，而C（﹣1，2），E（4，2）两点纵坐标相等，应该关于直线x=1对称，但C（﹣1，2）与对称轴相距2，E（4，2）与对称轴相距3，故不可能；（2）假设A点在抛物线上，得出矛盾排除A点在抛物线上；（3）B、D两点关于对称轴x=1对称，一定在抛物线上，另外一点可能是C点或E点，分别将C、D或D、E两点坐标代入求a和k的值．