题目内容
【题目】如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E. 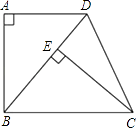
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
【答案】
(1)证明:∵AD∥BC,
∴∠ADB=∠EBC.
∵CE⊥BD,∠A=90°,
∴∠A=∠CEB,
在△ABD和△ECB中,
∵∠A=∠CEB,AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠BCE,
又∵BC=BD
∴△ABD≌△ECB
(2)解:∵∠DBC=50°,BC=BD,
∴∠EDC= ![]() (180°﹣50°)=65°,
(180°﹣50°)=65°,
又∵CE⊥BD,
∴∠CED=90°,
∴∠DCE=90°﹣∠EDC=90°﹣65°=25°.

【解析】(1)因为这两个三角形是直角三角形,BC=BD,因为AD∥BC,还能推出∠ADB=∠EBC,从而能证明:△ABD≌△ECB.(2)因为∠DBC=50°,BC=BD,可求出∠BDC的度数,进而求出∠DCE的度数.
【考点精析】关于本题考查的直角梯形,需要了解一腰垂直于底的梯形是直角梯形才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目




