题目内容
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
已知:PH∥AE,PK∥BC,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
【答案】
(1)解:如图所示,∵OE=80米,OC=ED=100米,AE=60米,BC=70米,
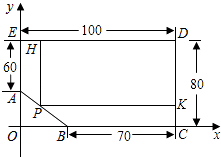
∴OA=20米,OB=30米,
即A、B的坐标为(0,20)、(30,0).
设直线AB的解析式为y=kx+b(k≠0),则 ![]() ,
,
解得, 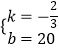 ,
,
则直线AB的解析式为y=﹣ ![]() x+20;
x+20;
(2)解:设点P的坐标为P(x,y).
∵点P在直线AB上,所以点P的坐标可以表示为(x,﹣ ![]() x+20),
x+20),
∴PK=100﹣x,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+ ![]() x,
x,
∴S=(100﹣x)(60+ ![]() x).
x).
【解析】根据题意容易求出A、B的坐标,利用待定系数法可以求出直线AB的解析式;(2)设点P的坐标为P(x,y),则PK=100﹣x,,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+![]() x,,根据矩形的面积公式可以求得函数解析式。
x,,根据矩形的面积公式可以求得函数解析式。
【考点精析】关于本题考查的确定一次函数的表达式和矩形的性质,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目