题目内容
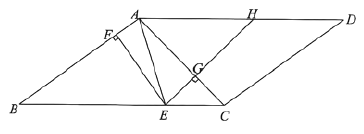
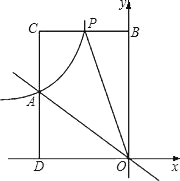
【题目】如图,已知正方形ABCD,点E在BA延长线上,点F在BC上,且∠CDE=2∠ADF.
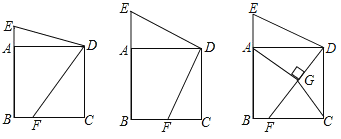
(1)求证:∠E=2∠CDF;
(2)若F是BC中点,求证:AE+DE=2AD;
(3)作AG⊥DF于点G,连CG.当CG取最小值时,直接写出AE:AB的值.
【答案】(1)详见解析;(2)详见解析;(3)1:2
【解析】
(1)如图1,延长BC至M,使得CM=AE,连接DM,根据正方形性质得出AB=BC=AD=CD,然后进一步证明△ADE△CDM,据此利用全等三角形性质以及正方形性质进一步分析求证即可;
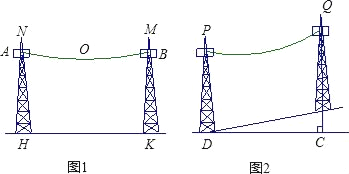
(2)如图2,延长BC至M,使得CM=AE,连接DM,作MH⊥DF于H,设BF=FC=x,利用勾股定理求出DF=![]() x,据此进一步分析证明△DFC~△MFH,最后再利用相似三角形性质进一步加以分析求证即可;
x,据此进一步分析证明△DFC~△MFH,最后再利用相似三角形性质进一步加以分析求证即可;
(3)如图3﹣1中,取AD的中点N,首先求出当C、G、N三点共线时,CG最小,然后如图3﹣2中,当C、G、N共线时,延长BC至M,使得CM=AE,连接DM,通过证明四边形NCMD为平行四边形进一步求解即可.
(1)证明:如图1,延长BC至M,使得CM=AE,连接DM,
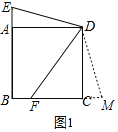
∵四边形ABCD为正方形,
∴AB=BC=AD=CD,
在△ADE与△CDM中,
∵AD=CD,∠DAE=∠DCM,AE=CM,
∴△ADE△CDM(SAS),
∴∠E=∠M,∠EDA=∠CDM,
∴∠CDE=∠ADM,
∵∠CDE=2∠ADF,
∴∠ADM=2∠ADF,
∴∠FDM=∠ADF,
∵正方形ABCD中AD∥BC,
∴∠ADF=∠DFM=∠FDM,
∴∠E=∠M=180°﹣2∠DFM,
∵∠DCB=90°,
∴∠CDF=90°﹣∠DFM,
∴∠E=2∠CDF.
(2)证明:如图2,延长BC至M,使得CM=AE,连接DM,作MH⊥DF于H.
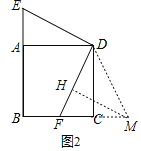
∵若F是BC中点,设BF=FC=x,则CD=2x,
在Rt△FDC中,DF=![]() x,
x,
由(1)得,∠DFM=∠FDM,
∴DM=FM,
又∵HM⊥DF,
∴FH=![]() DF=
DF=![]() x,
x,
∵∠DFC=∠MFH,∠DCB=∠MHF=90°,
∴△DFC~△MFH,
∴![]() ,
,
∴FM=![]() x,
x,
∴CM=AE=FM﹣FC=![]() x,
x,
∵DE=DM=FM=![]() x,
x,
∴AE+DE=![]() x+
x+![]() x=4x,
x=4x,
∵CD=AD=2x,
∴AE+DE=2AD.
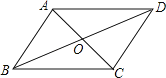
(3)如图3﹣1中,取AD的中点N.

∵AG⊥DF于点G,
∴∠AGD=90°,
∵AN=DN,
∴GN=![]() AD,
AD,
∵CG≥CN﹣GN,
∴当C、G、N三点共线时,CG最小.
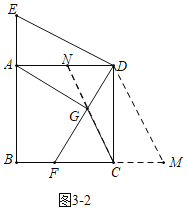
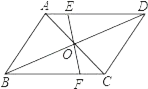
如图3﹣2中,当C、G、N共线时,延长BC至M,使得CM=AE,连接DM,
∵∠AGD=90°,N为AD中点,
∴AN=NG=ND,
∴∠NGD=∠ADF,
由(1)∠ADF=∠FDM,
∴∠NGD=∠FDM,
∴DM∥NC,
∵正方形ABCD中AD∥BC,
∴四边形NCMD为平行四边形,
∴CM=DN=![]() AD,
AD,
∵CM=AE,
∴AE=![]() AD=
AD=![]() AB,
AB,
∴AE:AB=1:2.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案