题目内容
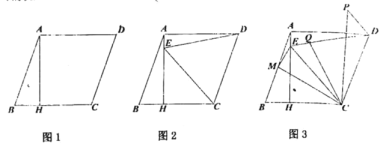
【题目】如图,![]() 中,点
中,点![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 于
于![]() ,已知
,已知![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() .
.
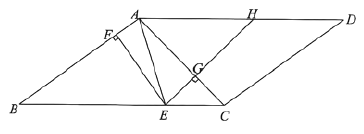
【答案】(1)∠BEA=70°;(2)证明见解析;
【解析】
(1)作BJ⊥AE于J.证明BJ是∠ABE的角平分线即可解决问题.
(2)作EM⊥AD于M,CN⊥AD于N,连接CH.证明△AEF≌△AEM(HL),△AGE≌△HGC(SAS),△EMA≌△CNH(HL),即可解决问题.
(1)解:作BJ⊥AE于J.
∵BF⊥AB,
∴∠ABJ+∠BAJ=90°,∠AEF+∠EAF=90°,
∴∠ABJ=∠AEF,
∵四边形ABCD是平行四边形,
∴∠D=∠ABC,
∵∠D=2∠AEF,
∴∠ABE=2∠AEF=2∠ABJ,
∴∠ABJ=∠EBJ,
∵∠ABJ+∠BAJ=90°,∠EBJ+∠BEJ=90°,
∴∠BAJ=∠BEJ,
∵∠BAE=70°,
∴∠BEA=70°.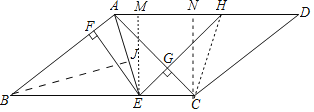
(2)证明:作EM⊥AD于M,CN⊥AD于N,连接CH.
∵AD∥BC,
∴∠DAE=∠BEA,
∵∠BAE=∠BEA,
∴∠BAE=∠DAE,
∵EF⊥AB,EM⊥AD,
∴EF=EM,
∵EA=EA,∠AFE=∠AME=90°,
∴Rt△AEF≌Rt△AEM(HL),
∴AF=AM,
∵EG⊥CG,
∴∠EGC=90°,
∵∠ECG=45°,
∠GCE=45°,
∴GE=CG,
∵AD∥BC,
∴∠GAH=∠ECG=45°,∠GHA=∠CEG=45°,
∴∠GAH=∠GHA,
∴GA=GH,
∵∠AGE=∠CGH,
∴△AGE≌△HGC(SAS),
∴EA=CH,
∵CM=CN,∠AME=∠CNH=90°,
∴Rt△EMA≌Rt△CNH(HL),
∴AM=NH,
∴AN=HM,
∵△ACN是等腰直角三角形,
∴AC=![]() AN,即AN=
AN,即AN=![]() AC,
AC,
∴AH=AM+HM=AF+![]() AC.
AC.