题目内容
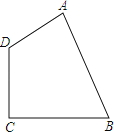
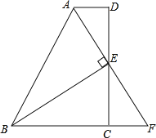
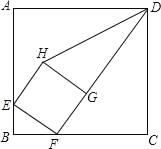
【题目】如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.
(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
【答案】(1)证明见试题解析;(2)![]() .
.
【解析】
试题(1)由正方形的性质得到∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.由∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,得到 ∠EFB =∠FDC.故△EBF∽△FCD;
(2)在Rt△CDF中,由勾股定理得到DF的长,由△EBF∽△FCD,得到 BE的长,再由勾股定理得到GH=的长,由于DG=DF-FG=![]() ,故可得到 tan∠HDG的值.
,故可得到 tan∠HDG的值.
试题解析:(1)证明:∵ 正方形ABCD,正方形EFGH,∴∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.又∵ 点F在BC上,点G在FD上,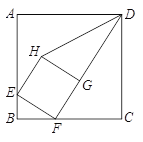

 ∴∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴∠EFB =∠FDC.∴△EBF∽△FCD;
∴∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴∠EFB =∠FDC.∴△EBF∽△FCD;
(2)解:∵BF=3,BC=CD=12,
 ∴CF=9,DF=
∴CF=9,DF=![]() ,由(1)得
,由(1)得![]() ,∴BE=
,∴BE=![]() ,∴GH=FG=EF=
,∴GH=FG=EF=![]() ,DG=DF-FG=
,DG=DF-FG=![]() ,∴tan∠HDG=
,∴tan∠HDG=![]() .
.

练习册系列答案
相关题目