��Ŀ����
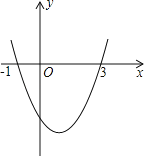
����Ŀ����ͼ��������y��ax2+bx+c��a��0���ĶԳ���Ϊֱ��x��1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ�
��b2��4ac��0��
�ڷ���ax2+bx+c��0����������x1����1��x2��3��
��2a+b��0��
�ܵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3��
�ݵ�x��0ʱ��y��x�������С��
���н�����ȷ�ĸ����ǣ�������
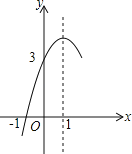
A.4��B.3��C.2��D.1��
���𰸡�B
��������
������������x��Ľ�������ɶԢٽ����жϣ����������ߵĶԳ��Եõ���������x���һ����������Ϊ��3��0������ɶԢڽ����жϣ��ɶԳ��᷽�̵õ�b����2a����ɶԢ۽����жϣ�������������x���Ϸ�����Ӧ���Ա����ķ�Χ�ɶԢܽ����жϣ����ݶ��κ��������ʶԢݽ����жϣ�
����ͼ����x����2�����㣬��b2��4ac��0���ʢٴ���
�����ĶԳ�����x��1������x�����һ�������ǣ�3��0����
��ax2+bx+c��0����������x1����1��x2��3���ʢ���ȷ��
�����ĶԳ�����x����![]() ��1����2a+b��0�������ʢ���ȷ��
��1����2a+b��0�������ʢ���ȷ��
������x��Ľ����ǣ���1��0���ͣ�3��0����y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3���ʢ���ȷ��
��x��1ʱ��y��x���������С����ݴ���
��ѡ��B��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�