ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»τΙΊ”Ύ x ΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χaxbxc=0Θ®a0Θ§c0Θ§aΓΔbΓΔcΈΣ≥Θ ΐΘ©”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυ![]() Θ§
Θ§![]() Θ®0
Θ®0![]()
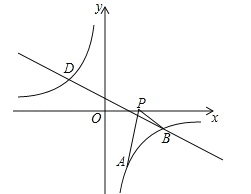
![]() Θ©Θ§OΈΣΉχ±ξ‘≠ΒψΘ§AΓΔBΈΣx÷α’ΐΑκ÷α…œΒΡΝΫΒψ«“A
Θ©Θ§OΈΣΉχ±ξ‘≠ΒψΘ§AΓΔBΈΣx÷α’ΐΑκ÷α…œΒΡΝΫΒψ«“A![]() Θ§0Θ§B
Θ§0Θ§B![]() Θ§0.
Θ§0.
Θ®1Θ©Β±![]() =c=2,b=-
=c=2,b=-![]() ±Θ§«σ
±Θ§«σ![]() ”κaΒΡ÷Β;
”κaΒΡ÷Β;
Θ®2Θ©Β± x 1Θ§c 6a ±Θ§PΈΣ“Μ¥ΈΚ· ΐ y x4ΆΦœσ…œ“ΜΒψΘ§QΈΣΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒΡ“ΜΒψΘ§»τΒψ AΓΔBΓΔPΓΔQ ΈΣ“ΜΗωΨΊ–ΈΒΡΥΡΗωΕΞΒψΘ§«κ»ΖΕ®ΒψQΒΡΉχ±ξΘΜ
Θ®3Θ©Β±![]() =2c ±Θ§ ‘Έ ‘Ύ’ΐ±»άΐΚ· ΐy=
=2c ±Θ§ ‘Έ ‘Ύ’ΐ±»άΐΚ· ΐy=![]() ΒΡΆΦœσ…œ «Ζώ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘΩ≈–Εœ≤Δ÷ΛΟςΡψΒΡΫα¬έΓΘ
ΒΡΆΦœσ…œ «Ζώ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘΩ≈–Εœ≤Δ÷ΛΟςΡψΒΡΫα¬έΓΘ

ΓΨ¥πΑΗΓΩΘ®1Θ©![]() =3Θ§a=
=3Θ§a=![]() ΘΜΘ®2Θ©ΒψQΒΡΉχ±ξΈΣΘΚΘ®6Θ§3Θ©ΜρΘ®1Θ§-2Θ©ΘΜΘ®3Θ©≤Μ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§÷ΛΟςΦϊΫβΈω.
ΘΜΘ®2Θ©ΒψQΒΡΉχ±ξΈΣΘΚΘ®6Θ§3Θ©ΜρΘ®1Θ§-2Θ©ΘΜΘ®3Θ©≤Μ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§÷ΛΟςΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©Α―![]() =c=2Θ§b=
=c=2Θ§b=![]() ¥ζ»κΩ…«σ≥ωaΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΗΟΖΫ≥ΧΘ§άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒΩ…«σ≥ωΝμ“ΜΗυΘΜ
¥ζ»κΩ…«σ≥ωaΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΗΟΖΫ≥ΧΘ§άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒΩ…«σ≥ωΝμ“ΜΗυΘΜ
Θ®2Θ©Α―x1Θ§c6a¥ζ»κΩ…«σ≥ωb=-7aΘ§¥”ΕχΫΪΖΫ≥Χ±δ–ΈΈΣa(x-1)(x-6)=0Θ§ΒΟΒΫAΘ§BΉχ±ξΘ§»ΜΚσΗυΨί“Μ¥ΈΚ· ΐΆΦœώ…œΒψΒΡΉχ±ξΧΊ’ςΚΆΨΊ–ΈΒΡ–‘÷ Ω…Ζ÷«ιΩω«σ≥ωΒψQΒΡΉχ±ξΘΜ
Θ®3Θ©ΫΪ![]() =2c¥ζ»κaxbx c=0άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒ«σ≥ω
=2c¥ζ»κaxbx c=0άϊ”ΟΗυ”κœΒ ΐΒΡΙΊœΒ«σ≥ω![]() Θ§ΒΟΒΫAΘ§BΉχ±ξΘ§ΙΐΒψMΉςMCΓΆx÷α”ΎΒψCΘ§”…C «AB÷–ΒψΘ§Ω…«σ≥ωCΒΡΉχ±ξΘ§ΫχΕχ¥ζ»κ’ΐ±»άΐΚ· ΐΫβΈω ΫΒΟΒΫMΒψΉχ±ξΘ§»ΜΚσΗυΨίCM=
Θ§ΒΟΒΫAΘ§BΉχ±ξΘ§ΙΐΒψMΉςMCΓΆx÷α”ΎΒψCΘ§”…C «AB÷–ΒψΘ§Ω…«σ≥ωCΒΡΉχ±ξΘ§ΫχΕχ¥ζ»κ’ΐ±»άΐΚ· ΐΫβΈω ΫΒΟΒΫMΒψΉχ±ξΘ§»ΜΚσΗυΨίCM=![]() ACΝ–≥ωΖΫ≥Χ«σ≥ωb÷ΒΘ§ΆΤ≥ωΟ§ΕήΘ§Έ ΧβΒΟΫβ.
ACΝ–≥ωΖΫ≥Χ«σ≥ωb÷ΒΘ§ΆΤ≥ωΟ§ΕήΘ§Έ ΧβΒΟΫβ.
ΫβΘΚΘ®1Θ©Α―![]() =c=2Θ§b=
=c=2Θ§b=![]() ¥ζ»κax bx c=0ΒΟΘΚ4a+2ΓΝ(
¥ζ»κax bx c=0ΒΟΘΚ4a+2ΓΝ(![]() )+2=0Θ§
)+2=0Θ§
ΫβΒΟΘΚa=![]() Θ§
Θ§
Υυ“‘ΗΟΖΫ≥ΧΈΣΘΚ![]() x
x![]() x 2=0Θ§
x 2=0Θ§
ΓΏ![]() =
=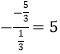 Θ§Φ¥2+
Θ§Φ¥2+![]() =5Θ§
=5Θ§
Γύ![]() =3ΘΜ
=3ΘΜ
Θ®2Θ©Α―x1Θ§c6a¥ζ»κaxbx c=0ΒΟab6a=0Θ§
Γύb=-7aΘΜ
Γύax-7ax 6a=0Θ§Φ¥a(xx 6)=0Θ§
Γύa(x-1)(x-6)=0Θ®a0Θ©Θ§
Γύ![]() Θ§
Θ§![]() Θ§
Θ§
ΓύA(1Θ§0)Θ§B(6Θ§0)Θ§
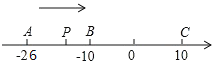
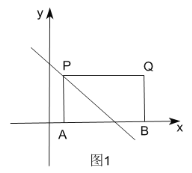
ΔΌ»γΆΦ1Θ§ΙΐΒψAΉςAPΓΆx÷αΫΜ÷±œΏyx4”ΎΒψPΘ§
ΓύPΘ®1Θ§3Θ©Θ§
ΓΏΥΡ±Ώ–ΈAPQBΈΣΨΊ–ΈΘ§
ΓύQΘ®6Θ§3Θ©ΘΜ
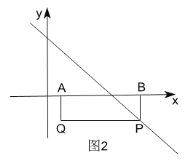
ΔΎ»γΆΦ2Θ§ΙΐΒψBΉςBPΓΆx÷αΫΜ÷±œΏyx4”ΎΒψPΘ§
ΓύPΘ®6Θ§-2Θ©Θ§
ΓΏΥΡ±Ώ–ΈABPQΈΣΨΊ–ΈΘ§
ΓύQΘ®1Θ§-2Θ©ΘΜ
Ήέ…œΥυ ωΘ§ΒψQΒΡΉχ±ξΈΣΘΚΘ®6Θ§3Θ©ΜρΘ®1Θ§-2Θ©ΘΜ
Θ®3Θ©≤Μ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘΜ
÷ΛΟςΘΚΫΪ![]() =2c¥ζ»κaxbx c=0ΒΟΘΚ4ac2+2bc+c=0Θ§Φ¥c(4ac+2b+1)=0Θ§
=2c¥ζ»κaxbx c=0ΒΟΘΚ4ac2+2bc+c=0Θ§Φ¥c(4ac+2b+1)=0Θ§
ΓΏc0Θ§
Γύ4ac+2b+1=0ΔΌΘ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύA(2cΘ§0)Θ§B(![]() Θ§0)Θ§
Θ§0)Θ§
ΦΌ…η¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
»γΆΦ3Θ§ΙΐΒψMΉςMCΓΆx÷α”ΎΒψCΘ§‘ρC «AB÷–ΒψΘ§
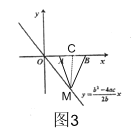
ΓύCΒψΚαΉχ±ξΈΣΘΚ![]() Θ§
Θ§
ΫΪ![]() ¥ζ»κ
¥ζ»κ![]() Ω…ΒΟ
Ω…ΒΟ![]() Θ§
Θ§
”…ΔΌΩ…÷Σ4ac=-(2b+1)Θ§4ac+1=-2bΘ§
Γύ![]() Θ§
Θ§
ΓύMΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Β±ΓςABMΈΣΒ»±Ώ»ΐΫ«–Έ ±Θ§CM=![]() ACΘ§
ACȧ
AC![]() Θ§
Θ§
Γύ![]()
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚb=-1Θ®…αΘ©Μρb=![]() Θ§
Θ§
ΓΏb=![]() Θ§
Θ§![]() Θ§
Θ§
ΓύaΘΦ0Θ§”κΧβ…η÷–a0Ο§ΕήΘ§
Γύ≤Μ¥φ‘ΎΒψM ΙΒΟΓςABMΈΣΒ»±Ώ»ΐΫ«–Έ.