题目内容
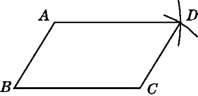
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,平移中的△ABF为△A1B1F1设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).
①当点F分别平移到线段AB上时,求出m的值
②当点F分别平移到线段AD上时,当直接写出相应的m的值.
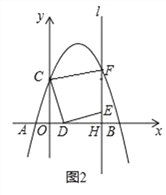
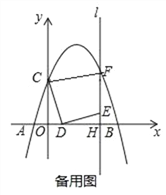
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AE交于点O,当∠A′BD=∠FAB时,请直接写出OB的长.
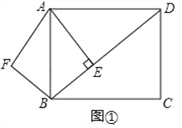
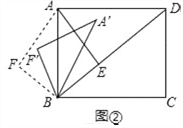
【答案】(1)AE=4,BE=3;(2)①3;②![]() ;(3)1或
;(3)1或![]() .
.
【解析】分析:(1)利用矩形性质、勾股定理及三角形面积公式求解;(2)依题意画出图形,如答图2所示.利用平移性质,确定图形中的等腰三角形,分别求出m的值;(3)在旋转过程中,分两种情形分别求解即可.
本题解析:
(1)在Rt△ABD中,AB=5,AD=![]() ,
,
由勾股定理得:BD=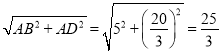 .
.
∵S△ABD=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=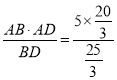 =4.
=4.
在Rt△ABE中,AB=5,AE=4,由勾股定理得:BE=3.
(2)设平移中的三角形为△A′B′F′,如答图2所示:
由对称点性质可知,∠1=∠2.
由平移性质可知,AB∥A′B′,∠4=∠1,BF=B′F′=3.
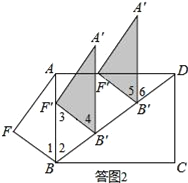
①当点F′落在AB上时,
∵AB∥A′B′,∴∠3=∠4,∴∠3=∠2,
∴BB′=B′F′=3,即m=3;
②当点F′落在AD上时,
∵AB∥A′B′,∴∠6=∠2,
∵∠1=∠2,∠5=∠1,∴∠5=∠6,
又易知A′B′⊥AD,
∴△B′F′D为等腰三角形,∴B′D=B′F′=3,
∴BB′=BD﹣B′D=![]() ﹣3=
﹣3=![]() ,即m=
,即m=![]() .
.
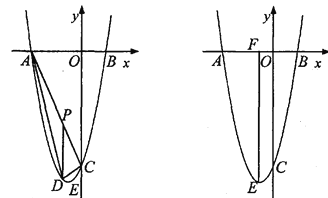
(3)如图3中,设AE交BA′于K.
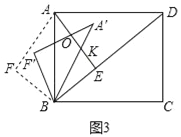
∵∠KBE=∠FAB=∠BAE,∠KEB=∠AEB,
∴△EKB∽△EBA,∴可得BE2=EKEA,∴EK=![]() ,
,
在Rt△BEK中,BK=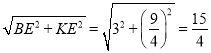 ,
,
∴A′K=5﹣![]() =
=![]() ,∵∠A′=∠KBE,∴OA′∥BE,∴
,∵∠A′=∠KBE,∴OA′∥BE,∴![]() ,
,
∴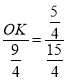 ,∴OK=
,∴OK=![]() ,∴AO=AE﹣OK=KE=1.
,∴AO=AE﹣OK=KE=1.
如图4中,当∠DBA′=∠BAF时,点A′在线段BC上,
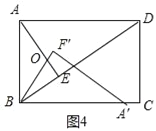
易证∠OAB=∠OBA,∴OA=OB,设OA=OB=x,
在Rt△OBE中,∵OB2=OE2+BE2,∴x2=32+(4﹣x)2,
∴x=![]() ,∴OA=
,∴OA=![]() ,
,
综上所述,满足条件的OA的长为1或![]() .
.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案