题目内容
【题目】如图,等腰△ABC中,AB=AC,P为其底角平分线的交点,将△BCP沿CP折叠,使B点恰好落在AC边上的点D处,若DA=DP,则∠A的度数为( ) 
A.20°
B.30°
C.32°
D.36°
【答案】D
【解析】解:连接AP, 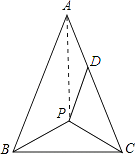
∵P为其底角平分线的交点,
∴点P是△ABC的内心,
∴AP平分∠BAC,
∵AB=AC,
∴∠ABC=∠ACB,
设∠A=2x,则∠DAP=x,∠PBC=∠PCB=45°﹣ ![]() x,
x,
∵DA=DP,
∴∠DAP=∠DPA,
由折叠的性质可得:∠PDC=∠PBC=45°﹣ ![]() x,
x,
则∠ADP=180°﹣∠PDC=135°+ ![]() x,
x,
在△ADP中,∠DAP+∠DPA+∠ADP=180°,即x+x+135°+ ![]() x=180°,
x=180°,
解得:x=18,
则∠A=2x=36°.
故选D.
【考点精析】本题主要考查了等腰三角形的性质和翻折变换(折叠问题)的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

练习册系列答案
相关题目