题目内容
【题目】 如图,两块形状、大小完全相同的三角板按照如图所示的样子放置,找一找图中是否有互相平行的线段,完成下面证明:
证明:
∵∠______=∠______,
∴______∥______(______)(填推理的依据)
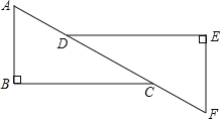
【答案】A ;F; AB;EF;内错角相等,两直线平行(或“ACB;FDE;BC;DE;内错角相等,两直线平行”)
【解析】
直接利用平行线的判定方法分析即可得出答案.
解法1:证明:∵∠A=∠F,
∴AB∥EF( 内错角相等,两直线平行).
解法2:证明:∵∠ACB=∠FDE,
∴BC∥DE( 内错角相等,两直线平行).
故答案为:A;F;AB;EF;内错角相等,两直线平行(或“ACB;FDE;BC;DE;内错角相等,两直线平行”).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.