题目内容
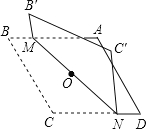
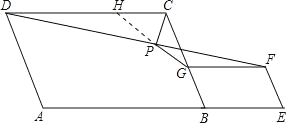
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,已知AB=BC,BG=BE,点A,B,E在同一直线上,P是线段DF的中点,连接PG,PC,若∠DCB=∠GEF=120°,则![]() =( )
=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
可通过构建全等三角形求解.延长GP交DC于H,可证三角形DHP和FGP全等,已知的有DC∥GF,根据平行线间的内错角相等可得出两三角形中两组对应的角相等,又有DP=PF,因此构成了全等三角形判定条件中的(AAS),于是两三角形全等,那么HP=PG,可根据三角函数来得出PG、CP的比例关系.
解:延长GP交DC于点H,
∵AB=BC,BG=BE,
∴平行四边形ABCD和平行四边形BEFG都是菱形,
∵P是线段DF的中点,
∴FP=DP,
由题意可知DC∥GF,
∴∠GFP=∠HDP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GP=HP,GF=HD,
∵四边形ABCD是菱形,
∴CD=CB,
∴CG=CH,
∴△CHG是等腰三角形,
∴PG⊥PC,(三线合一)
又∵∠DCB=∠GEF=120°,
∴∠ABC=∠BEF=60°,
∴∠GCP=60°,
∴![]() =
=![]() .
.
故选:B.

练习册系列答案
相关题目